제이의 집

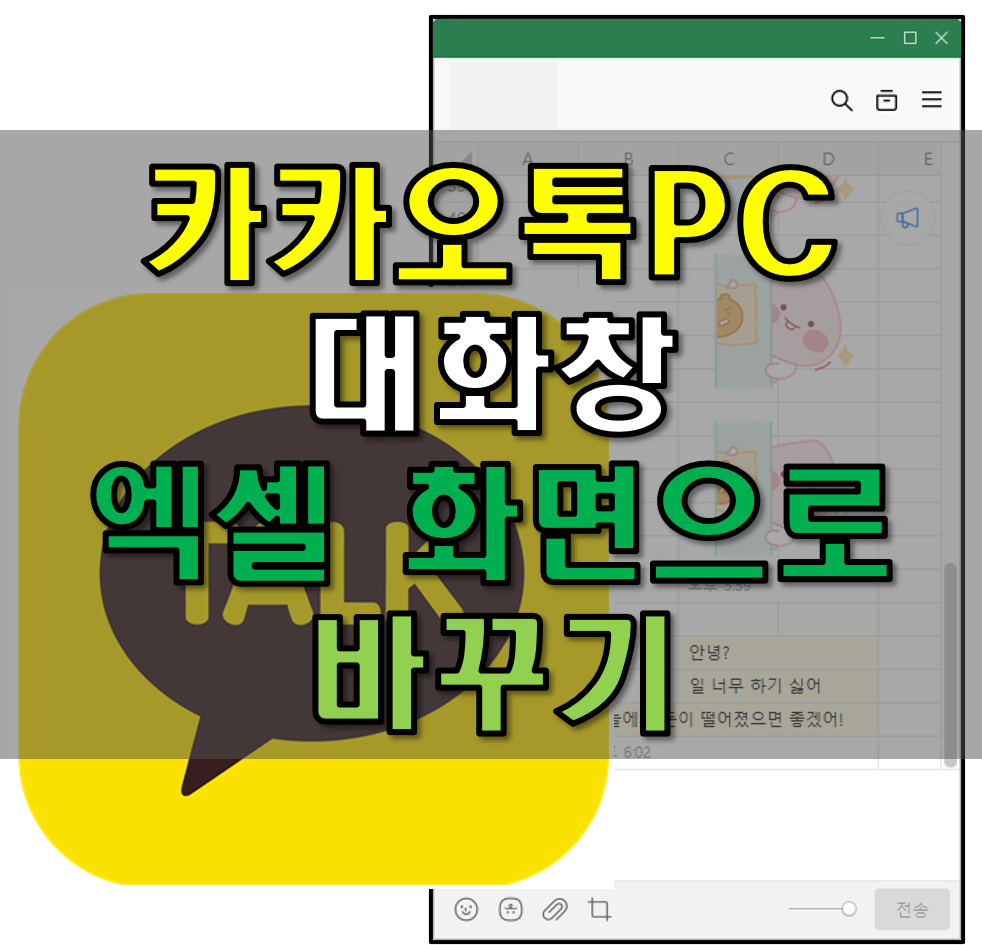
Program : 카카오톡 PC 회사에서 업무 시 연락을 주고받아야 할 때가 많다. 필자 같은 경우는 아웃룩 메일을 주고받지만 경우에 따라서는 카카오톡도 주고받는 것 같다. 그런데 대부분 사람들의 연락수단 중 하나인 카카오톡을 업무시간에 업무시에만 사용하는 경우는 잘 없을 것이다. 친구들이나 애인들이랑도 카톡을 주고받고 해야 할 것인데 회사에서 하기에는 눈치가 좀 보이기 마련이다. 이에 대하여 조금은 도움이 되는 기능을 소개하려고 한다. 이번 글에서는 카카오톡 PC 대화창 엑셀 화면으로 바꾸는 방법에 대하여 알아보자. 엑셀 화면으로 바꾸기 예전 대한민국 군복은 산에서 위장효과를 보기 위해 초록과 검정, 연두, 갈색 등이 섞인 모습이었다. 카카오톡 대화창을 엑셀화면으로 바꾼다는 것은 이와 비슷한 개념이라고..

절대값 기호가 있는 그래프 그리기 일반적으로 절대값 기호가 있는 함수의 그래프는 절대값 기호 안이 0이 되는 x의 값을 경계로 구간을 나누어 그린다.▼ 그리고 절대값 기호가 있는 그래프는 아래와 같은 절차를 밟아서 그려진다. 1. 절대값 안을 0으로 하는 x의 값을 구한다. 2. 구한 x의 값을 경계로 그 값보다 클 때와 작을 때로 구분. 3. 범위에 적합하도록 그래프를 그린다. 이 절차에 따라 그려진 그래프의 예시를 살펴보도록 하자. 절대값 함수 그래프의 예시 f(x) = x - 4 라고 두고 4가지 절대값 함수 그래프에 대하여 알아보자. 1. y = |f(x)| = |x - 4| x ≥ 4일 때, |f(x)| = x - 4, x

만나는 두 원의 방정식을 정의하면 이 둘이 만나는 교점을 지나는 원의 방정식은 아래와 같이 말할 수 있다.▼ ▲이 식의 핵심은 k ≠ -1이라는 것이다. 왜 그런지는 아래에서 후술 하도록 하겠다. 교점을 지나는 원을 그림으로 보면 아래와 같다.▼ ▲검은테두리 두 원이 만나는 교점을 지나는 빨간색깔의 원이 바로 위에서 구한 만나는 두 원의 교점을 지나는 원이다. k ≠ -1 인 이유? 왜 k ≠ -1 이어야 할까? 만약 k = -1 이라면 x², y² 항이 소거가 되어 원의 방정식이 만들어지지 않고 일차항으로만 이루어진 직선의 방정식이 만들어진다. 이 직선의 방정식은 두 원의 교점을 지나는 직선, 즉 공통현의 방정식이다. 자세한 내용은 아래의 글을 참조하도록 하자. 공통현의 방정식에 대하여 알아보자

App : Instagram 정확히 언제인지는 모르겠지만 인스타그램에 메모를 할 수 있는 기능이 생겼다. DM을 자주 이용하는 사람이라면 한 번쯤은 남들이 남긴 메모를 봤을 것이다. 이번 글에서는 인스타그램 메모 기능에 대하여 알아보자. 메모 기능 ▲메모 기능을 사용하는 방법은 정말 간단하다. 자신의 DM에 들어가서 메모 남기기를 누르면 된다. 누르자. ▲메모란에 적고 싶은 내용을 적으면 된다. 공유 대상은 맞팔로우 중인 사람과 친한 친구 목록 둘 중 하나를 선택할 수 있다. 혼자 보는 설정은 제공하지 않는 것 같다. ▲Test라고 내가 남긴 메모를 확인할 수 있다. 그리고 공유 대상을 맞팔로우인 사람으로 설정했으니 나의 Test메모는 다른 사람들도 볼 수 있다. ▲다시 나의 메모를 누르면 새 메모를 남..

원 밖의 한 점에서 그은 접선의 방정식을 구하는 방법은 크게 2가지가 있다. 1. 판별식 D를 이용 2. 원의 성질을 이용 두 방법 크게 계산상에 있어서 큰 차이가 없다. 이 차이가 없다는 말은 어떤 방식이 좀 더 계산하기 편리하다는 것에 대한 차이가 없다는 말이다. 자신에게 좀 더 익숙한 방법을 택하면 되겠다. 각 방법들에 대하여 살펴보도록 하자. 1. 판별식 D를 이용 점(2,0)에서 원 x²+y²=1에 그은 접선의 방정식을 구하여 보자. 우선 점(2,0)을 지나고 기울기가 m인 접선의 방정식을 정의하자.▼ 이 접선의 방정식을 x²+y²=1에 대입하고 x에 대하여 정리하자.▼ x에 대하여 정리된 식을 이제 판별식 D를 적용하여 다시 정리하여 그 식을 좀 전의 직선의 방정식에 대입하자.▼ ▲위와 같이 ..

Program : Microsoft Power Point 파워포인트는 PDF로 저장할 수 있다. 보통 파워포인트 파일로 슬라이드쇼를 하지만 PDF로 저장할 필요도 있지 않겠는가? 공식적인 메일을 주고받는 것이라면 대부분은 PDF파일로 전달된다. 이번 글에서는 파워포인트 PDF로 저장하는 방법에 대하여 알아보자. PDF로 저장하기 PDF로 저장하는 방법은 2가지가 있다. 1. 인쇄를 이용한 저장 ▲위와 같은 파워포인트 파일을 PDF로 저장해보자. 우선 왼쪽 윗 상단에 보이는 파일을 클릭하도록 하자. ▲여기서 망설이지 말고 인쇄를 클릭하도록 하자. ▲프린터의 설정을 "Microsoft Print to PDF"로 변경한 후 인쇄를 클릭하도록 하자. ▲저장할 PDF의 파일 이름을 지정할 수 있는 항목이 나온다...

공통현이란? 공통현이란 두 원이 두 점 A, B에서 만날 때 두 원의 교점을 연결한 선분을 말한다. 아래의 그림을 본다면 좀 더 이해가 쉬울 것이다. ▲두 원의 교점 A와 B를 잇는 선분 AB가 바로 공통현이다. ▲두 원의 중심 O, O'를 이은 중심선은 두 원의 공통현을 수직이등분한다. 따라서 위와 같이 말할 수 있다. ▲원의 성질을 조금만 생각하면 두 원의 공통현은 중심선에 의하여 수직이등분 된다는 사실을 증명할 수 있다. 공통현의 방정식 공통현이 무엇인지는 위에서 알아보았다. 그러면 이제 공통현의 방정식에 대하여 알아보자. 두 원의 방정식을 안다면 공통현의 방정식은 아래와 같이 아주 쉽게 구할 수 있다. ▲위와 같이 두 원의 방정식을 서로 빼면 된다. 그러면 이차항이 소거가 되어 일차식 즉, 직선의..

빛의 반사의 법칙 빛이 진행하다가 다른 매질의 경계면에서 반사할 때, 2가지 현상이 나타난다. 1. 입사 광선과 반사 광선은 법선의 양쪽에 있고 두 광선은 법선과 동일 평면 내에 있다. 2. 입사각과 반사각의 크기는 같다. 표현하면 ∠i = ∠i' 이다. 이것을 반사의 법칙이라고 한다. 정반사 ▲거울면처럼 매끄러운 곳에 평행한 빛이 입사를 하면 반사되는 빛 또한 평행 광선이 된다. 이것을 정반사라고 부른다. 즉, 정반사는 반사의 법칙에 따라 반사가 되는 것을 말한다. 난반사 ▲사실 우리 일상에서는 정반사는 보기 힘들다. 대부분 물체의 표면은 매끄럽지 않기 때문이다. 이러한 물체 표면에 빛이 입사하면 빛이 닿은 각각의 입사점에서 반사의 법칙에 따라 반사하지만 각각 광선은 서로 다른 방향으로 나아간다. 이렇..

산술평균, 기하평균, 조화평균 산술평균, 기하평균, 조화평균. 이 셋은 유명한 절대부등식으로써 수포자가 아니라면 정말 많이 들어본 단어일 것이고 또 그만큼 많이 쓰이는 내용이다. 절대부등식이니 당연히 부등식 관련 문제에서 많이 나오며, 두 수의 합이나 곱의 최댓값, 최솟값 등을 구하는 경우 많이 쓰인다. 식은 다음과 같다. ▲필자가 한창 수학 공부를 하던 시절에는 조화평균은 거의 접한 적이 없었다. 그렇다고 숙지를 안한건 아니었다. 산술평균과 기하평균은 지겹게 봤을 것이다. 저게 왜 성립을 할 수 있을까? 증명을 해보자. 증명하기 굉장히 많이 나오는 내용이라 뭔가 증명하는 방법도 화려할 것 같은 느낌이 들지만 의외로 간단한 사칙연산을 통하여 손쉽게 증명이 가능하다. ▲위와 같이 식 ①, ②같은 관계를 알..

코시-슈바르츠의 부등식 사람은 죽어서 이름을 남긴다는 말이 있다. 수학자로 불리는 사람들은 공식을 만들어서 이름을 남긴다. 공식의 이름은 그 수학자의 이름으로 불리기 때문이다. 코시-슈바르츠 부등식도 마찬가지다. 코시와 슈바르츠라는 두 사람이 만든 부등식이다. 코시-슈바르츠의 부등식은 아래와 같다. ▲수학을 공부하는 사람은 절대 모르면 안 되는 부등식 중 하나다. 굉장한 응용력을 가진 부등식이기 때문에 거의 전 분야에서 활용이 가능하다고 생각하면 된다. 증명하기 증명하는 방법은 어렵지 않다. 식을 풀어서 전개하면 금방 이해할 수 있다. ▲증명하는 방법 자체는 단순하지만 계산 과정은 이래저래 어렵지는 않아도 좀 귀찮다. 공식을 반드시 암기하도록 하자.