
| 절대값 기호가 있는 그래프 그리기 |
일반적으로 절대값 기호가 있는 함수의 그래프는 절대값 기호 안이 0이 되는 x의 값을 경계로 구간을 나누어 그린다.▼

그리고 절대값 기호가 있는 그래프는 아래와 같은 절차를 밟아서 그려진다.
1. 절대값 안을 0으로 하는 x의 값을 구한다.
2. 구한 x의 값을 경계로 그 값보다 클 때와 작을 때로 구분.
3. 범위에 적합하도록 그래프를 그린다.
이 절차에 따라 그려진 그래프의 예시를 살펴보도록 하자.
| 절대값 함수 그래프의 예시 |
f(x) = x - 4 라고 두고 4가지 절대값 함수 그래프에 대하여 알아보자.
1. y = |f(x)| = |x - 4|
x ≥ 4일 때, |f(x)| = x - 4, x < 4일 때, |f(x)| = - x + 4 이므로 그래프를 그리면 아래와 같다.▼

▲y = f(x)를 그린 후, x축 윗부분과 x축 아랫부분을 x축에 대칭이동한 부분을 그리면 된다.
2. y = f(|x|) = |x| - 4
x ≥ 0일 때, f(|x|) = x - 4, x < 0일 때, |f(x)| = - x - 4 이므로 그래프를 그리면 아래와 같다.▼

▲y = f(x)를 그린 후, y축의 오른쪽 부분과 y축의 오른쪽 부분을 y축에 대칭이동한 부분을 그리면 된다.
3. |y| = f(x) = x - 4
y ≥ 0일 때, f(x) = x - 4, y < 0일 때, f(x) = - x + 4 이므로 그래프를 그리면 아래와 같다.▼
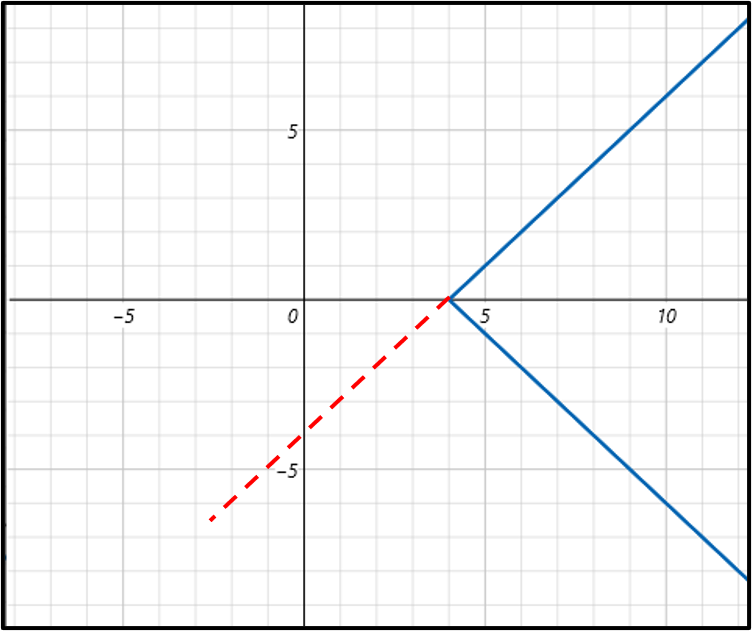
▲y = f(x)를 그린 후, x축의 윗부분과 x축의 윗부분을 x축에 대칭이동한 부분을 그리면 된다.
4. |y| = f(|x|) = |x| - 4
x ≥ 0, y ≥ 0 일 때 |y| = f(|x|) = x - 4, x ≥ 0, y < 0 일 때 |y| = f(|x|) = - x + 4
x < 0, y ≥ 0 일 때 |y| = f(|x|) = - x - 4, x < 0, y < 0 일 때 |y| = f(|x|) = x + 4
총 4가지 경우가 나온다.▼
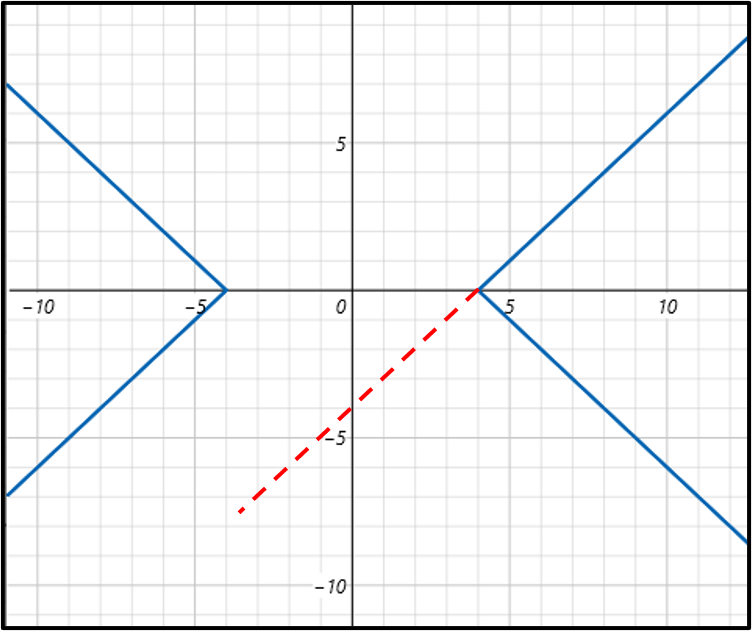
▲y = f(x)에서 제 1사분면만 그리고 이것을 x축, y축, 원점에 대칭이동하여 그리자.
'수학이야기 > 이론' 카테고리의 다른 글
| 이차방정식의 실근의 부호 조건 및 그래프 (1) | 2023.02.26 |
|---|---|
| 지수함수와 지수함수 그래프의 특징 (0) | 2023.02.11 |
| 두 원의 교점을 지나는 원의 방정식에 대하여 알아보자 (0) | 2023.02.04 |
| 원 밖의 한 점에서 그은 접선의 방정식 구하기 (0) | 2023.02.02 |
| 공통현의 방정식에 대하여 알아보자 (0) | 2023.01.31 |