반응형

| 지수함수란? |
a가 1인 아닌 양수일 때, 실수 x에 ax을 대응시키는 함수를 지수함수라고 한다.
표현하면 y=ax (a ≠ 1, a > 0) 이것을 a를 밑으로 하는 지수함수라고 한다.
반응형
| 지수함수 그래프의 성질 |
y=ax는 a > 1인 경우와 0 < a < 1인 경우 2가지로 나누어 생각할 수 있다.
이 2가지 경우를 그래프로 나타내면 아래와 같다.▼
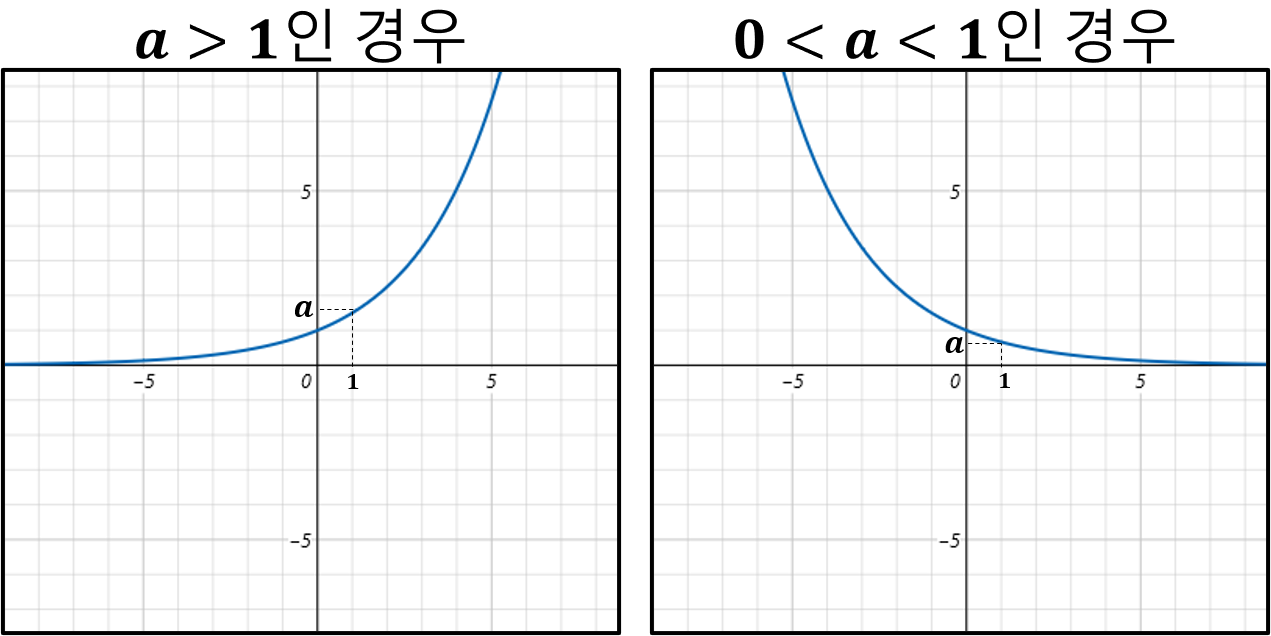
지수함수 그래프는 아래와 같은 성질을 가지고 있다.
1. 정의역은 실수 전체의 집합, 치역은 양의 실수 전체 집합이다.
2. 그래프는 점 (0,1), (1, a)를 지나고 x축(y = 0)을 점근선으로 한다.
3. a > 1일 때, x의 값이 증가하면 y의 값은 증가한다. 반면 0 < a < 1일 때, x의 값이 증가하면 y값은 감소한다.
이 사실은 위 그래프로 잘 표현이 되어 있다.
4. y = ax 그래프와 y=(1/a)x의 그래프는 y축에 대하여 대칭이다.
5. 대소를 비교할 경우, a > 1일 때, 즉 밑이 1보다 클 때는 지수가 큰 수가 크다.
반대로 0 < a < 1일 때, 즉 밑이 0보다 크고 1보다 작을 때는 지수가 작은 수가 크다.
위 5가지 사항은 그리 어려운 내용은 아니다. 하지만 굉장히 중요한 원리적인 내용이니 반드시 익혀두도록 하자. 그래프를 대강이라도 직접 그려보면 좀 더 이해하기가 수월하다.

| ※ 함께 읽기 실수의 대소에 대한 기본 성질 및 증명하기 절대값 기호가 있는 함수의 그래프에 대하여 알아보자 |
반응형
'수학이야기 > 이론' 카테고리의 다른 글
| 미정계수법 - 계수비교법, 수치대입법 (0) | 2023.02.27 |
|---|---|
| 이차방정식의 실근의 부호 조건 및 그래프 (1) | 2023.02.26 |
| 절대값 기호가 있는 함수의 그래프에 대하여 알아보자 (0) | 2023.02.05 |
| 두 원의 교점을 지나는 원의 방정식에 대하여 알아보자 (0) | 2023.02.04 |
| 원 밖의 한 점에서 그은 접선의 방정식 구하기 (0) | 2023.02.02 |