제이의 집

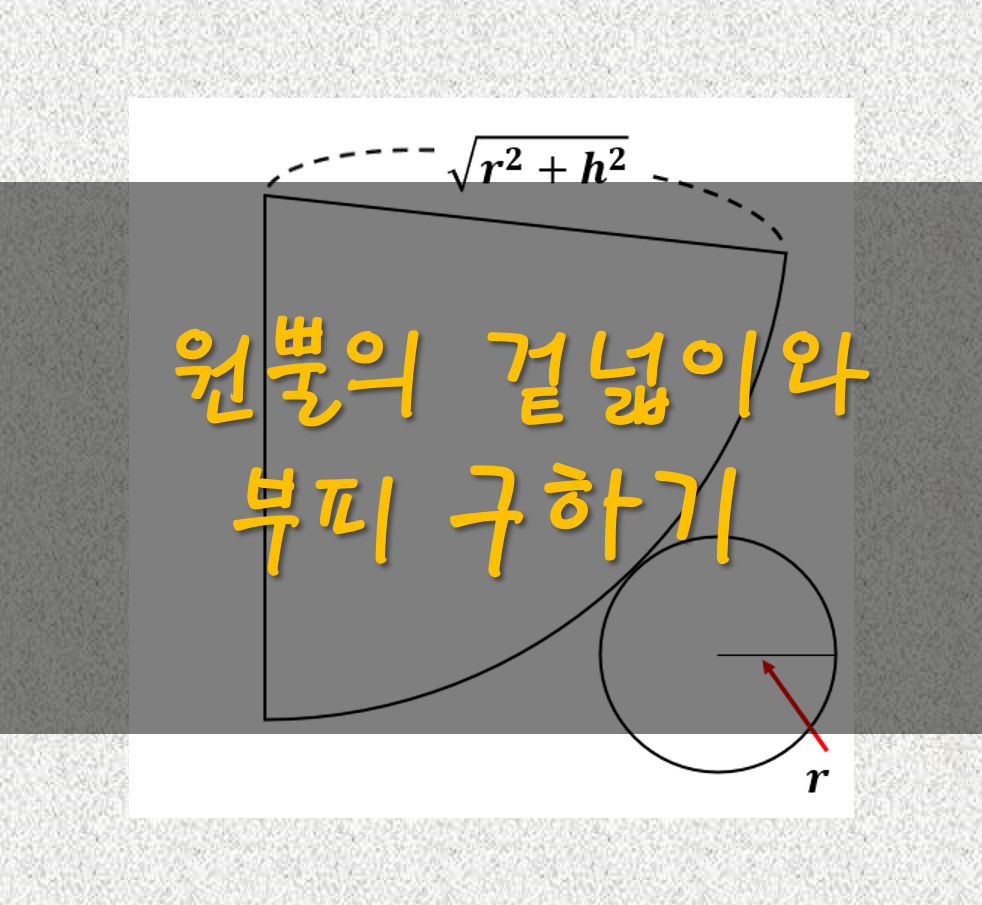
개요 원뿔은 많이 접하게 되는 입체 도형중 하나다. 문제에서도 상당히 단골로 나오는 도형이기도 하다. 이번 글에서는 원뿔의 겉넓이와 부피 공식을 차례대로 살펴보도록 하겠다. 원뿔의 겉넓이 공식 원뿔의 겉넓이는 결국 원뿔의 옆면 + 원뿔의 밑면의 값이다. 아래와 같은 원뿔이 주어진다면 겉넓이는 다음과 같이 말할 수 있다. 밑면은 결국 원의 넓이니까 그리 어려운 내용이 아니다. 원의 넓이 구하는 방법을 모르겠다면 원의 둘레(원주)와 원의 넓이 구하기←클릭 문제는 옆면의 넓이를 구하는 것이다. 원뿔의 옆면은 모선을 반지름으로 하는 부채꼴의 넓이라는 것을 알 수 있다. 그럼 여기서 부채꼴의 넓이를 구하는 방법을 잠깐 살펴보자. 부채꼴의 넓이 구하는 식에는 부채꼴의 반지름과 호의 길이가 포함되어있다. 이것을 원뿔..

부채꼴의 호의 길이 공식 아래와 같은 부채꼴이 있을 때, 호의 길이는 다음과 같은 식으로 나타낼 수 있다. 부채꼴의 넓이는 다음과 같이 나타낼 수 있다. 증명하기 어쩌면 공식보다도 중요한 것이 호의 길이 공식, 부채꼴의 넓이 유도 과정이라고 생각된다. 유도 과정에서 쓰이는 내용이 꽤 복잡한 문제에서 의외로 활약하기 때문이다. 증명의 핵심은 호의 길이는 중심각의 크기에 비례하다는 것, 그리고 부채꼴의 넓이 또한 중심각의 크기에 비례한다는 것이다. 아니 이게 다라고 보면 된다. 아니 이게 다다. 우선 원주와 원은 넓이를 구하는 공식부터 알아야 한다. 원주와 원의 넓이를 구하는 방법은 아래 글을 참고하지. →원의 둘레(원주)와 원의 넓이 구하기 내용을 익혔다면 각도가 2π일때의 경우 비례식을 세우자. 각도가 ..

외접원의 반지름의 길이를 알 때 삼각형의 넓이 다음 그림을 보자. 이 경우에 삼각형의 넓이는 아래와 같이 쓸 수 있다. 증명하기 이 공식을 증명하기 위해서는 2가지의 사전 지식이 필요하다. 1. 두 변과 그 끼인각을 알 때 삼각형의 넓이 공식 및 증명하기 2. 사인 법칙에 대하여 알아보고 증명하자 이 2가지를 알고 있다면 증명할 수 있다. 우선 두 변과 그 끼인각을 알 때의 넓이 공식부터 시작한다.

사인법칙이란? 사인법칙은 삼각형과 외접원에서 적용시킬 수 있는 공식이다. △ABC의 세 각의 크기 A, B, C와 세 변의 길이 a, b, c 및 외접원의 반지름의 길이 R에서는 아래와 같은 식이 성립된다. 이를 사인법칙이라고 부르며, 경우에 따라 식을 조금 변형해서 쓰기도 한다. 코사인 법칙과 마찬가지로 삼각함수에서 상당히 많이 쓰이는 공식 중 하나이다. 증명하기 사인법칙 증명의 핵심은 어떠한 삼각형에서라도 성립이 된다는 것을 보여야 한다. 삼각형은 크게 예각삼각형, 둔각삼각형, 직각삼각형이 있으니 각각의 삼각형에서 사인법칙을 성립시킬 수 있다는 것을 보여주자. △ABC의 외접원의 중심을 O, 반지름의 길이를 R, 반지름선분BO의 연장선과 원 O의 교점을 A'라고 하면 선분BA=2R이 된다. 이제 삼각..

삼각함수의 덧셈정리란? 삼각함수의 덧셈정리... 상당히 많이 활용되는 공식이다. sin, cos, tan에 대하여 아래와 같이 말할 수 있다. 이때 α, β는 주어진 식의 각을 분해하여 특수각으로 나타낸다. 특수각에 관한 내용은 아래 글을 참고하자. 삼각함수 특수각의 삼각비의 값 삼각함수 특수각의 삼각비의 값 정말 많은 분야에서 쓰이는 삼각함수. 그 중에서도 많이 쓰이는 특수각의 삼각비의 값을 알아보자. 수학공부를 하는 사람이라면 윗 표 내용은 구구단외듯이 숙지하고 다니자. houseofj.tistory.com 증명하기 증명하는 방법은 여러 가지가 있지만 이번 글에서는 좌표평면을 이용하여 증명해보겠다. 아래의 그림을 보자. 그림처럼 좌표평면 위의 단위원과 x축의 양의 부분을 시초선으로 하는 각들, 단위원..

이등변삼각형 넓이 공식 아래 그림과 같은 삼각형을 보자. 두 변의 길이가 b로 같고 다른 한 변의 길이가 a인 이등변 삼각형이 있다. 이 경우 이등변삼각형 넓이 공식은 아래와 같이 쓸 수 있다. 이 공식은 대체 어떻게 나오는 걸까? 알아보도록 하자. 공식 유도하기 위 삼각형에서 높이만 알 수 있다면 밑 변의 길이를 곱해서 넓이를 구할 수 있다. 그렇다면 삼각형의 높이를 구해보자. 가운데 꼭지점에서 수직으로 선을 그으면 직각삼각형 하나가 만들어진다. 여기서 피타고라스의 정리를 사용하면 쉽게 높이를 구할 수 있다. 높이를 구해보자. 높이를 구했다. 삼각형의 넓이는 밑 변 X 높이 X 1/2 이므로 계산하면 공식이 완성된다. 거창한 말로 공식이라고 표현을 하지만 사실 그냥 정석적인 방법으로 삼각형을 높이를 구..

자취의 방정식이란? 점의 자취란 일정한 조건에서 점이 움직일 때, 그 점의 집합 전체가 이루는 도형을 말한다. 그렇다면 자취의 방정식은 이 점의 자취를 표현한 방정식이라고 말할 수 있겠다. 위 좌표평면에 그어진 선의 방정식은 x=1이다. 이 선은 x의 좌표가 1인 선들의 집합이라고 말할 수 있다. 다시 말하면 이 선을 나타내는 방정식 x=1은 x의 좌표가 1인 점들의 자취라고 말할 수 있는 것이다. 자취의 방정식을 구하는 방법 자취의 방정식은 특정한 조건을 만족하는 점의 자취를 구하는 식이다. 대부분의 자취의 방정식을 구하는 방법은 다음 과정에 따른다. 어떤 조건을 만족하는 점의 자취를 구한다면..... ① 조건을 만족하는 점의 좌표를 P(x, y)로 둔다. ② 주어진 조건을 이용하여 x와 y의 관계식을..

점과 직선 사이의 거리 공식 점 P(x₁, y₁)에서 직선 ax+by+c=0까지의 거리를 d라고 둔다면 d는 다음과 같은 공식으로 구할 수 있다. 거의 뭐 구구단처럼 많이 쓰이는 공식이니 꼭 알아둬야한다. 참고로 이 공식은 a=0 또는 b=0일 때도 성립하는 공식이다. 즉 직선 l이 x축 또는 y축에 평행일 때도 성립하는 공식이다. 그러면 이제 왜 이런 공식이 나오는 건지 알아보자. 증명하기 뭐 직선, 도형 등 기하와 관련된 공식들중 상당수는 좌표평면상에서 증명할 수 있다. 점과 직선 사이의 거리 공식도 마찬가지다. 아래의 그림을 보자. 한 점 P에서 직선 l에 그은 수선의 발을 H라고 할 때, 점 P와 직선 l사이의 거리는 선분 PH의 길이라고 말할 수 있다. 그리고 다음과 같이 표현할 수 있다. 두 ..

두 직선이 수직일 조건 임의의 두 직선이 수직이 된다면 다음과 같은 식이 성립된다. 이 조건은 상당히 많은 문제에서 응용이 되는 내용이니 잘 알고 있어야 한다. 증명하기 많은 공식이 기하학적으로 접근하면 쉽게 증명할 수 있는 경우가 많다. 이 내용도 그러하다. 아래의 그림을 보자. 위 그림과 같이 원점을 지나고 서로 수직인 두 직선을 긋고 직선 x=1을 그으면 교점 P, Q가 만들어지고 위에 표시된 좌표를 가지게 된다. 그리고 삼각형 △POQ가 만들어지고 ∠POQ = 90° 이므로 피타고라스의 정리를 활용할 수 있다. 정리해보자. 이 내용은 증명과정 보단 결과가 이용되는 경우가 참 많으니 그냥 이렇게 증명할 수 있구나 정도로만 기억하고 넘어가자. ※같이 보기 피타고라스의 정리 증명하기

개요 직선의 방정식은 일차함수로 이루어진 식이다. 간단한 함수이지만 이 직선의 방정식을 구하는 데는 여러 가지 공식이 있다. 문제에서 주어지는 조건에 따라 적용되는 직선의 방정식의 공식은 각각 다르다. 지금부터 어떠한 조건이 주어졌을때, 어떠한 공식을 적용시키면 되는지, 그리고 그 공식은 어떻게 나오게 된 것인지 증명을 해보도록 하겠다. 기울기가 m이고 한 점 A(x₁, y₁)을 지나는 직선의 방정식 이 경우에는 아래오 같은 공식으로 직선의 방정식을 구할 수 있다. 증명하는 방법은 아주 간단하다. 일반적인 직선의 방정식은 y=mx+n으로 표현할 수 있다. 이 식에다가 (x₁, y₁)를 집어넣어서 이쁘게 식을 정리해주면 증명은 끝난다. 우선 n을 고쳐서 정리해보자. 고쳐서 정리된 n을 다시 y=mx+n에 ..