| 사인법칙이란? |
사인법칙은 삼각형과 외접원에서 적용시킬 수 있는 공식이다. △ABC의 세 각의 크기 A, B, C와 세 변의 길이 a, b, c 및 외접원의 반지름의 길이 R에서는 아래와 같은 식이 성립된다.

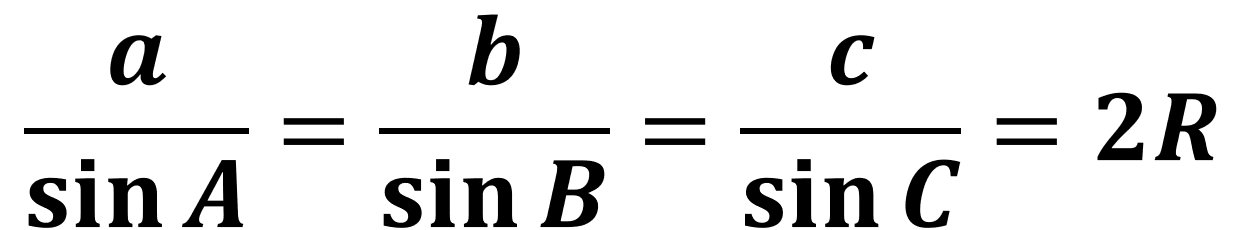
이를 사인법칙이라고 부르며, 경우에 따라 식을 조금 변형해서 쓰기도 한다.

코사인 법칙과 마찬가지로 삼각함수에서 상당히 많이 쓰이는 공식 중 하나이다.
| 증명하기 |
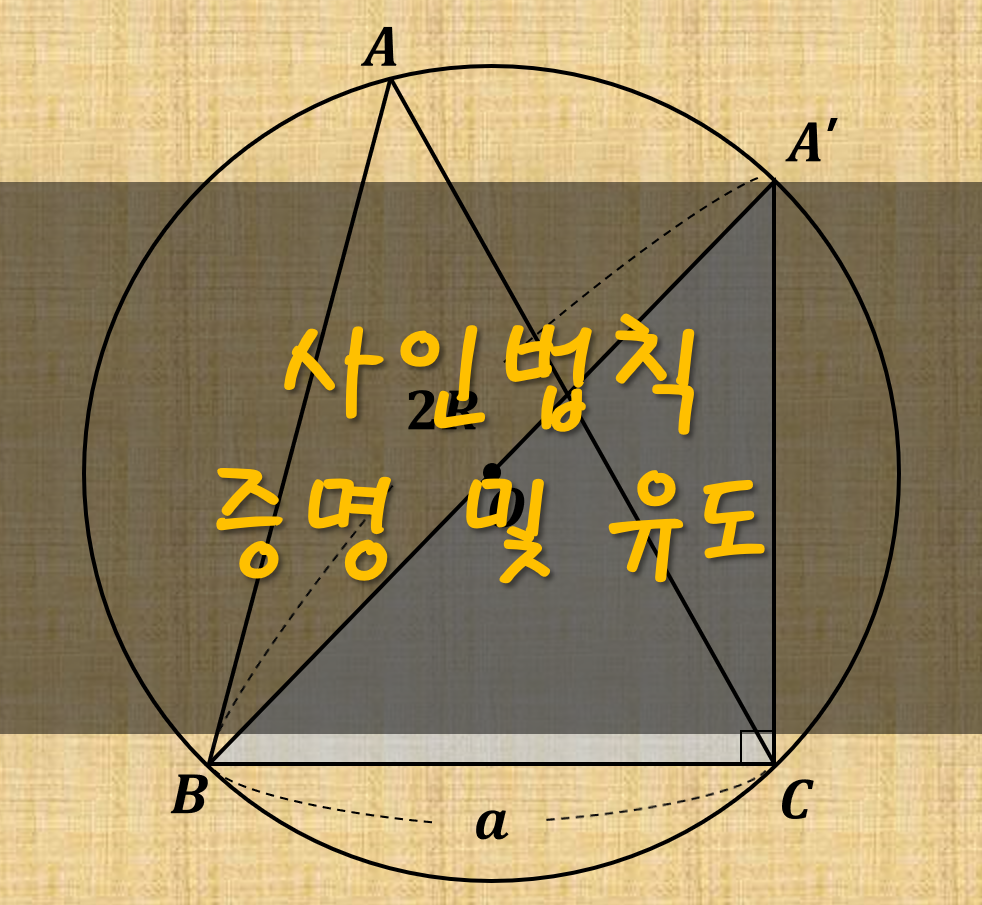
사인법칙 증명의 핵심은 어떠한 삼각형에서라도 성립이 된다는 것을 보여야 한다. 삼각형은 크게 예각삼각형, 둔각삼각형, 직각삼각형이 있으니 각각의 삼각형에서 사인법칙을 성립시킬 수 있다는 것을 보여주자.
△ABC의 외접원의 중심을 O, 반지름의 길이를 R, 반지름선분BO의 연장선과 원 O의 교점을 A'라고 하면 선분BA=2R이 된다. 이제 삼각형 하나하나마다 살펴보자.

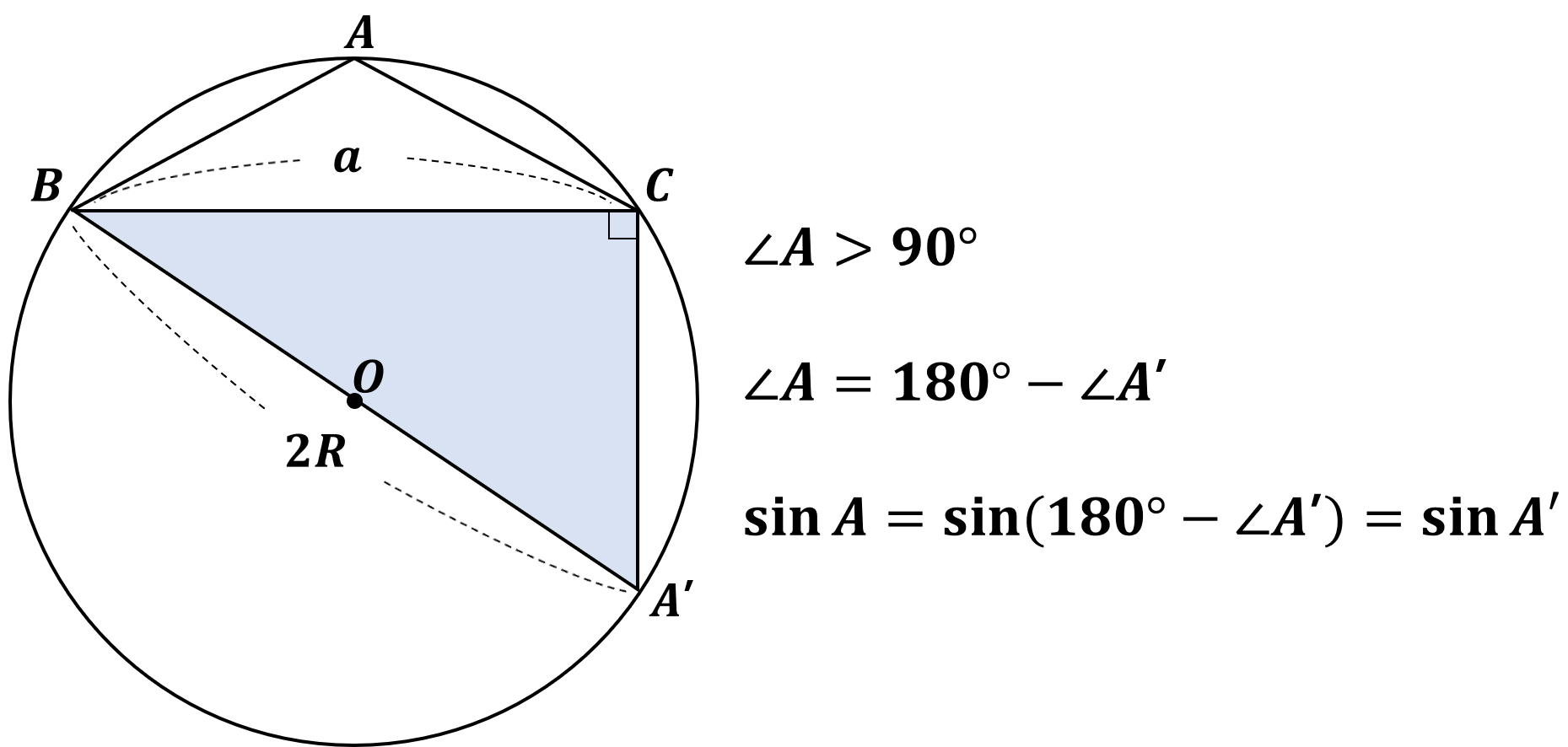


시험장에서 이것을 하나하나쓰면서 공식을 유도할 수는 없으니 머릿속에 잘 저장해두고 있자.
※같이 읽기
제1코사인법칙 및 유도과정에 대하여 알아보자
제1코사인법칙이란? 다음과 같은 삼각형이 있다고 보자 이때 아래와 같은 공식들이 성립한다. 이것을 제1코사인법칙이라고 한다. 제1코사인법칙 유도 과정 제1코사인법칙은 모든 삼각형에서 증
houseofj.tistory.com
제2코사인법칙 공식 및 유도과정
제2코사인법칙이란? 임의의 삼각형이 주어졌을 때, 제1코사인법칙과 제2코사인법칙이 성립된다. 다음과 같은 삼각형이 주어졌을 때 다음과 같은 식이 성립한다. 위의 식을 제2코사인법칙이라고
houseofj.tistory.com
'수학이야기 > 공식 모음' 카테고리의 다른 글
| 부채꼴의 호의 길이와 부채꼴의 넓이 공식 및 증명하기 (0) | 2021.11.20 |
|---|---|
| 외접원의 반지름의 길이를 알 때 삼각형의 넓이 구하기 (0) | 2021.11.19 |
| 삼각함수의 덧셈정리와 증명하기 (0) | 2021.11.15 |
| 이등변삼각형 넓이 공식 및 유도 (0) | 2021.11.13 |
| 자취의 방정식에 대하여 알아보자. (0) | 2021.11.12 |