반응형

| 제1코사인법칙이란? |
다음과 같은 삼각형이 있다고 보자

이때 아래와 같은 공식들이 성립한다.

이것을 제1코사인법칙이라고 한다.
| 제1코사인법칙 유도 과정 |
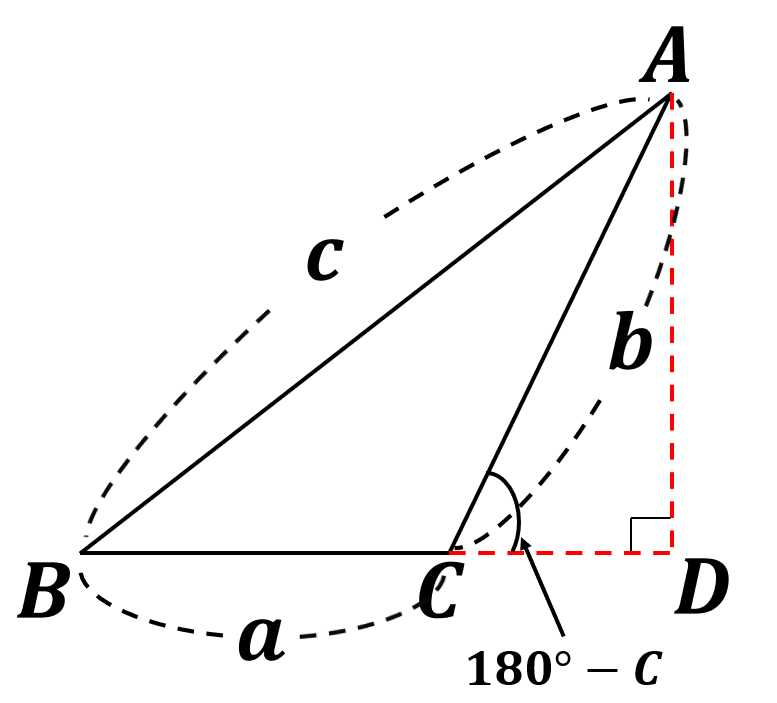
제1코사인법칙은 모든 삼각형에서 증명이 가능하다. △ABC의 꼭지점 A에서 밑변 또는 그 연장선 위에 내린 수선의 발을 D라고 한다면, 다음과 같이 식을 세울 수 있다.
1. 예각삼각형의 경우

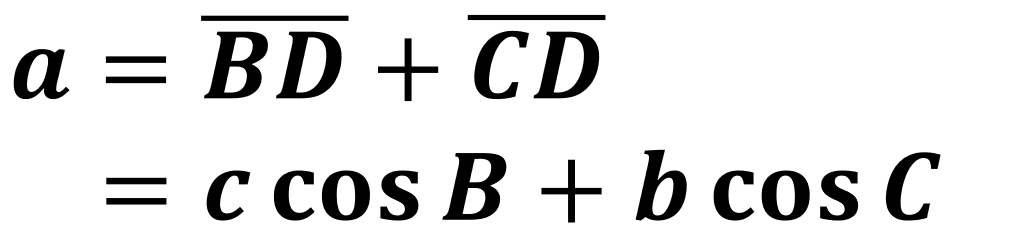
2. 둔각삼각형의 경우

여기서 삼각형의 보각 공식을 적용시키면
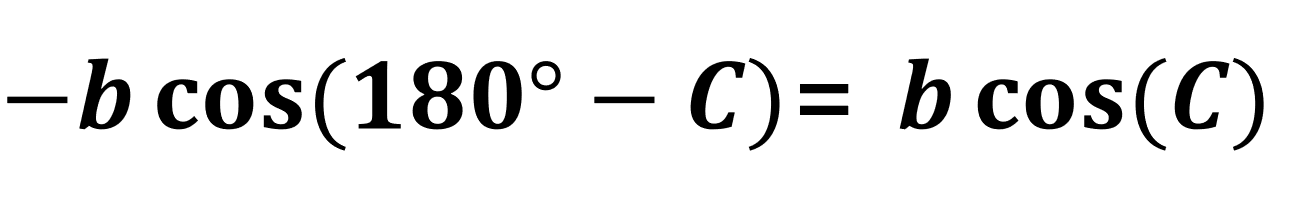
변환된 이 식을 다시 대입하면
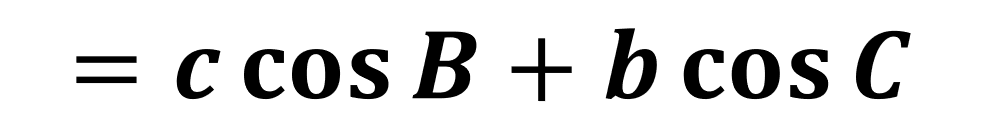
3. 직각삼각형
직각삼각형은 따로 수선의 발을 그을 필요가 없다. 직각이니까!


그런데 여기서 cos90°=0이므로 cosC는 = 0 이다. 따라서 아래처럼 표현을 다시 쓸 수 있다.

a뿐만 아니라 b, c도 같은 방법으로 표현이 가능하니, 위의 과정을 잘 보고 b와 c를 제1코사인법칙으로 표현하는 것은 여러분들의 몫으로 남기려고 한다. 아니 합니다.
반응형
'수학이야기 > 공식 모음' 카테고리의 다른 글
| 정사면체의 겉넓이, 높이, 부피 공식 및 유도 (0) | 2021.10.29 |
|---|---|
| 구의 겉넓이와 부피 구하기 (0) | 2021.10.28 |
| 다각형 대각선 개수 공식 및 유도하기 (0) | 2021.10.26 |
| 평행사변형 넓이 구하는 공식 및 유도 (0) | 2021.10.25 |
| 삼각함수의 변환 공식에 대하여 알아보자. (0) | 2021.10.24 |