
| 삼각함수의 덧셈정리란? |
삼각함수의 덧셈정리... 상당히 많이 활용되는 공식이다.
sin, cos, tan에 대하여 아래와 같이 말할 수 있다.

이때 α, β는 주어진 식의 각을 분해하여 특수각으로 나타낸다.
특수각에 관한 내용은 아래 글을 참고하자.
삼각함수 특수각의 삼각비의 값
정말 많은 분야에서 쓰이는 삼각함수. 그 중에서도 많이 쓰이는 특수각의 삼각비의 값을 알아보자. 수학공부를 하는 사람이라면 윗 표 내용은 구구단외듯이 숙지하고 다니자.
houseofj.tistory.com
| 증명하기 |
증명하는 방법은 여러 가지가 있지만 이번 글에서는 좌표평면을 이용하여 증명해보겠다.
아래의 그림을 보자.

그림처럼 좌표평면 위의 단위원과 x축의 양의 부분을 시초선으로 하는 각들, 단위원과의 교점 P, Q의 좌표를 알 수 있다.
여기서 ∠POQ=(α - β), 선분OP=1, 선분OQ=1이다.
여기서 △POQ에 제2코사인법칙을 적용하면

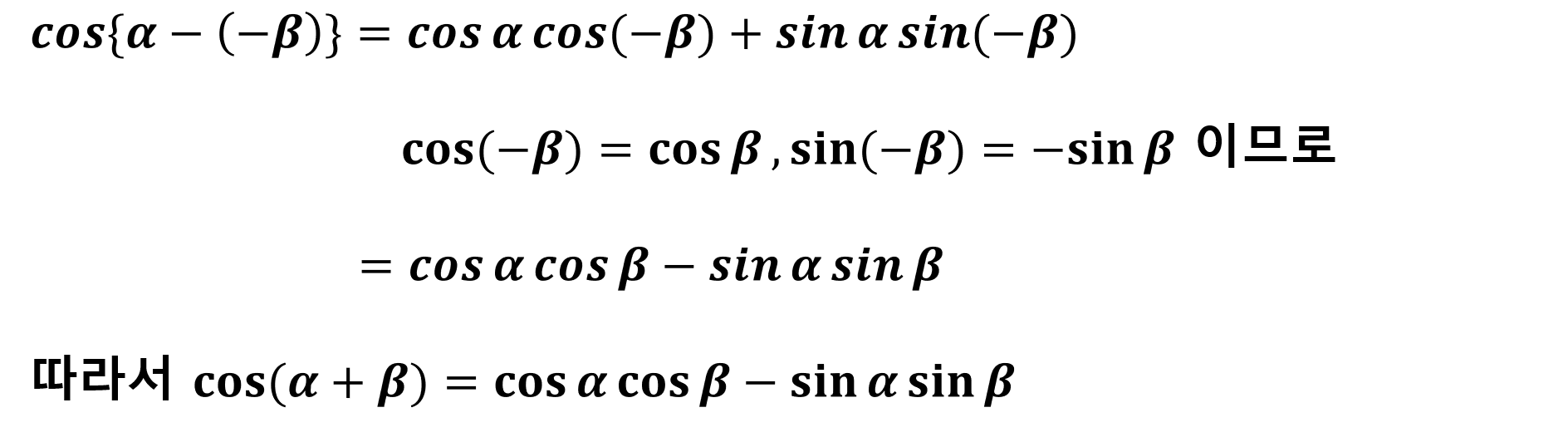
sin에 관련된 식도 cos에서 약간의 변형만 한다면 유도를 할 수 있다.

위에서 구한 cos, sin 덧셈정리를 활용하여 tan에 관한 덧셈정리를 구할 수 있다.

어려운 내용은 아니지만 귀찮은 계산들이 이것저것 있다.
구구단처럼 자주 쓰이는 공식이니 잘 기억해두자.
※참고 하기
제2코사인법칙 공식 및 유도과정
제2코사인법칙이란? 임의의 삼각형이 주어졌을 때, 제1코사인법칙과 제2코사인법칙이 성립된다. 다음과 같은 삼각형이 주어졌을 때 다음과 같은 식이 성립한다. 위의 식을 제2코사인법칙이라고
houseofj.tistory.com
삼각함수의 변환 공식에 대하여 알아보자.
개요 삼각함수의 변환 공식에는 크게 4가지가 있다. 1. 음각 공식 2. 주기 공식 3. 보각 공식 4. 여각 공식 이번 글에서는 각각의 공식에 대하여 알아보도록 하자. 1. 음각 공식 2. 주기 공식 3. 보각
houseofj.tistory.com
'수학이야기 > 공식 모음' 카테고리의 다른 글
| 외접원의 반지름의 길이를 알 때 삼각형의 넓이 구하기 (0) | 2021.11.19 |
|---|---|
| 사인 법칙에 대하여 알아보고 증명하자 (0) | 2021.11.18 |
| 이등변삼각형 넓이 공식 및 유도 (0) | 2021.11.13 |
| 자취의 방정식에 대하여 알아보자. (0) | 2021.11.12 |
| 점과 직선사이의 거리 공식 및 증명하기 (0) | 2021.11.11 |