| 개요 |
원뿔은 많이 접하게 되는 입체 도형중 하나다. 문제에서도 상당히 단골로 나오는 도형이기도 하다. 이번 글에서는 원뿔의 겉넓이와 부피 공식을 차례대로 살펴보도록 하겠다.
| 원뿔의 겉넓이 공식 |
원뿔의 겉넓이는 결국 원뿔의 옆면 + 원뿔의 밑면의 값이다.
아래와 같은 원뿔이 주어진다면 겉넓이는 다음과 같이 말할 수 있다.


밑면은 결국 원의 넓이니까 그리 어려운 내용이 아니다.
원의 넓이 구하는 방법을 모르겠다면
문제는 옆면의 넓이를 구하는 것이다. 원뿔의 옆면은 모선을 반지름으로 하는 부채꼴의 넓이라는 것을 알 수 있다.
그럼 여기서 부채꼴의 넓이를 구하는 방법을 잠깐 살펴보자.

부채꼴의 넓이 구하는 식에는 부채꼴의 반지름과 호의 길이가 포함되어있다. 이것을 원뿔로 끌어와서 생각해보자.
부채꼴의 반지름은 원뿔의 모선의 길이고 호의 길이는 밑면의 둘레 즉 밑면은 원이니 원주의 길이가 되는 것이다.
이 사실은 반드시 기억해야한다. 어렵지 않은 사실이지만 기억하지 못한다면 정말 낭패 본다....
그러면 이제 원뿔의 모선의 길이를 구해보자. 모선의 길이는 구하는 것은 간단하다.
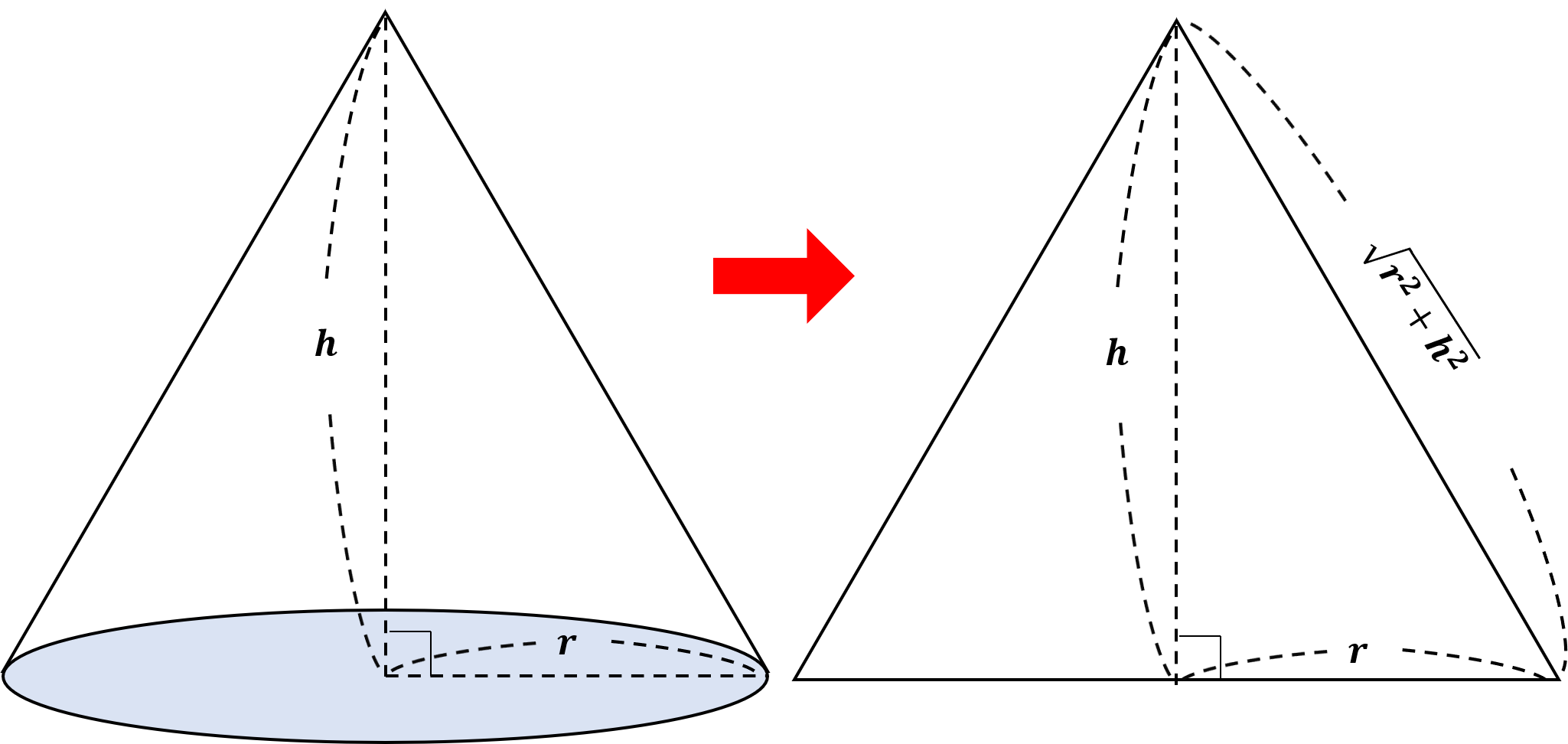
간단하게 피타고라스의 정리를 이용하며 모선의 길이를 쉽게 구할 수 있다. 모선의 길이를 구했다면 이제 원뿔을 펼쳐보자.
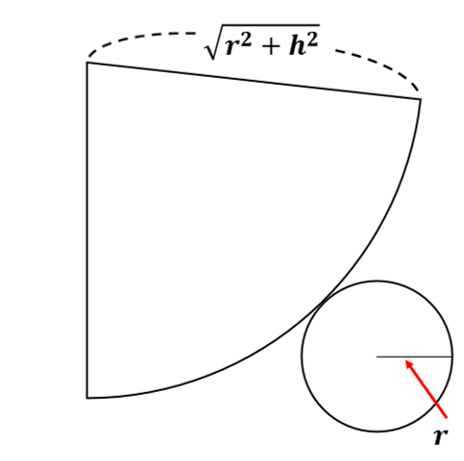
펼쳐보면 옆면은 부채꼴이라는 것을 확실하게 알 수 있으며 호의 길이는 밑면을 이루는 원의 원주, 부채꼴의 반지름은 모선의 길이라는 것을 다시 확인할 수 있다. 원주의 길이는 2πr 이다. 그럼 이제 옆면을 구하기 위한 모든 길이를 알게 되었으니 부채꼴의 넓이를 구하는 공식에 대입하여 적용시켜보자.

이렇게 해서 원뿔의 옆면의 넓이를 구하는 식을 끌어낼 수 있다.
| 원뿔의 부피 구하기 |
원뿔의 부피를 구하는 식은 잘 알려져 있다.
밑면의 넓이 X 높이 X 1/3 이므로 식으로 표현하면
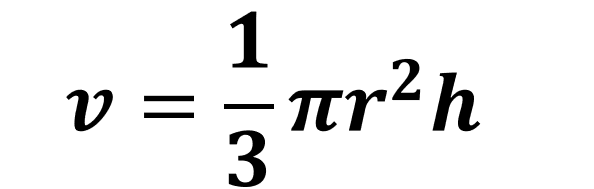
왜 3분의 1을 곱해야 하는지를 알고 싶다면 아래의 글을 참조하자.
뿔의 부피는 왜 기둥의 부피의 3분의1일까????
개요 모든 각뿔의 부피는 각기둥의 부피의 3분의 1을 곱하면 된다는 것을 어린 시절부터 배워왔을 것이다. 이 공식은 초중학교 시절에 배우는 것으로 기억하고 있는데 왜 이렇게 계산하면 되는
houseofj.tistory.com
'수학이야기 > 공식 모음' 카테고리의 다른 글
| 정사각뿔 높이, 겉넓이, 부피 구하는 공식 및 증명 (0) | 2021.12.14 |
|---|---|
| 공통외접선과 공통내접선의 길이 공식 및 증명하기 (0) | 2021.12.07 |
| 부채꼴의 호의 길이와 부채꼴의 넓이 공식 및 증명하기 (0) | 2021.11.20 |
| 외접원의 반지름의 길이를 알 때 삼각형의 넓이 구하기 (0) | 2021.11.19 |
| 사인 법칙에 대하여 알아보고 증명하자 (0) | 2021.11.18 |