
| 정사각뿔이란? |
정사각뿔은 밑면이 정사각형, 옆면이 이등변삼각형으로 이루어진 입체 도형을 말한다.
그림으로 보자면 아래와 같다.

▲수학공부를 하면서 자주 접하는 도형이기도 하다. 이번 글에서는 정사각뿔의 높이, 겉넓이, 부피 구하는 공식과 이에 대하여 증명하는 방법을 알아보도록 하겠다.
| 정사각뿔의 높이 |
정사각뿔의 높이 공식은 아래와 같다.

증명하는 방법은 어렵지 않다. 정사각뿔의 밑면에 선 하나를 그어보자.

▲밑면에 선 하나를 그으면 하늘색 삼각형이 하나 만들어진다. 오른쪽처럼 하늘색 삼각형을 따로 놓고 본다면 피타고라스의 정리를 활용하여 높이 h를 구할 수 있다. 그렇다면 저 하늘색 삼각형의 밑변의 길이는 어떻게 나온걸까?

▲이번에는 정사각뿔의 밑면을 따로 가져와보자. 위 그림같이 선이 그어진다면 직각이등변삼각형이 만들어진다. 여기서 삼각함수 공식을 통하여 변의 길이를 구할 수 있다.
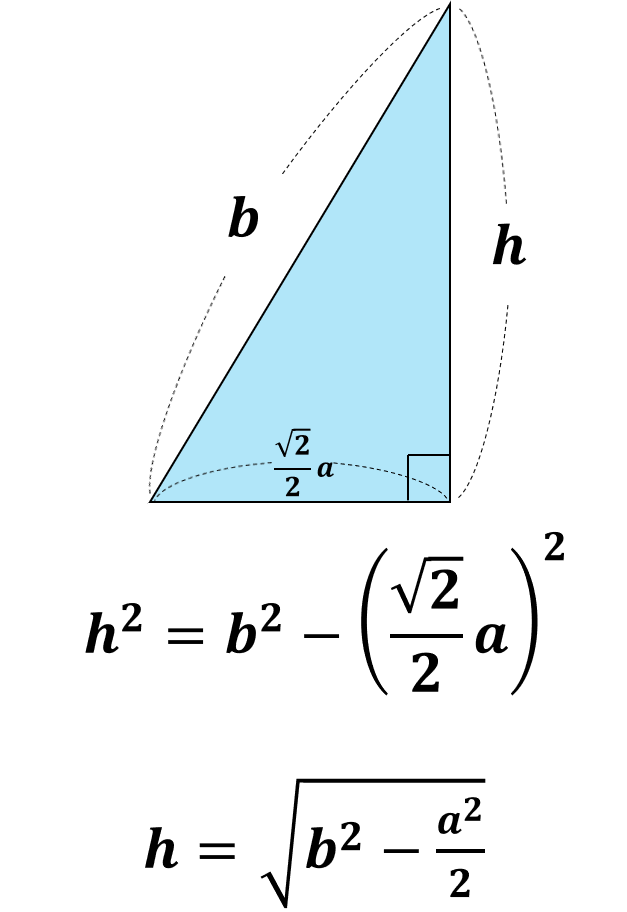
▲다시 하늘색 삼각형으로 돌아가서 피타고라스의 정리를 활용하면 높이 h는 위와 같이 구할 수 있다.
| 정사각뿔의 겉넓이 |
누구나 다 아는 사실이지만 겉넓이는 = 밑면의 넓이 + 옆면의 넓이다.
식으로 쓰면 아래와 같다.
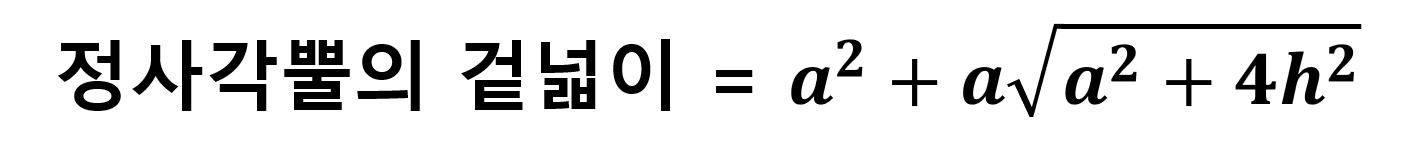
밑면의 넓이는 한 변의 길이가 a인 정사각형의 넓이니 a²으로 그리 어렵지 않게 구할 수 있다.
문제는 옆면의 넓이인데.... 옆면의 넓이는 결국 이등변삼각형 4개의 넓이의 합이라고 말할 수 있다. 그럼 이제 옆면을 이루고 있는 이등변삼각형 하나의 넓이를 구해보자.
우선 옆면을 하나 따로 가져와보자.

▲그림처럼 옆면 삼각형의 높이는 위와 같은 식으로 구할 수 있다. 높이를 구했으니 이제 밑면과 곱하여 삼각형의 넓이를 구할 수 있을 것이며 이 삼각형 4개의 넓이가 곧 정사각뿔 옆면의 넓이가 된다. 정리하면...

| 정사각뿔의 부피 |
부피 공식은 아래와 같다.
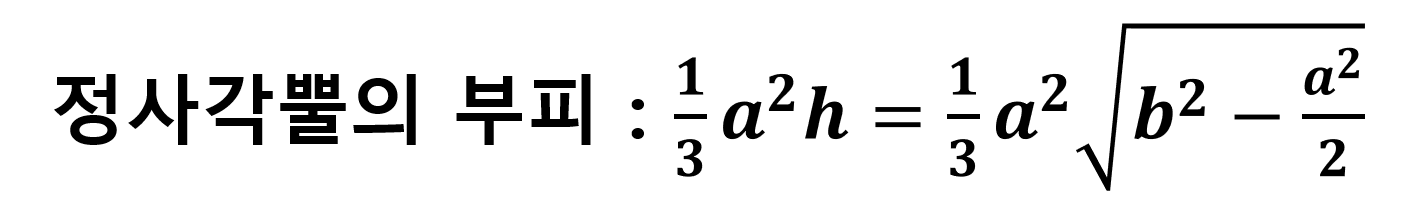
▲기본적으로 입체 도형의 부피는 밑면의 넓이 X 높이 X 1/3 이다. 정사각뿔 역시 마찬가지이며 높이 h는 앞서 구한 값을 대입시키면 완성된다. 왜 부피 계산에는 X 1/3이 들어가는지 알고 싶다면 아래의 글을 참조하자.
'수학이야기 > 공식 모음' 카테고리의 다른 글
| 삼수선의 정리와 증명하는 방법 (0) | 2022.04.01 |
|---|---|
| 직육면체 대각선 길이 공식 및 증명하기 (0) | 2021.12.15 |
| 공통외접선과 공통내접선의 길이 공식 및 증명하기 (0) | 2021.12.07 |
| 원뿔의 겉넓이와 부피 공식 및 증명하기 (0) | 2021.11.24 |
| 부채꼴의 호의 길이와 부채꼴의 넓이 공식 및 증명하기 (0) | 2021.11.20 |