
| 개요 |
모든 각뿔의 부피는 각기둥의 부피의 3분의 1을 곱하면 된다는 것을 어린 시절부터 배워왔을 것이다. 이 공식은 초중학교 시절에 배우는 것으로 기억하고 있는데 왜 이렇게 계산하면 되는지에 대한 것은 배우지 않았을 것이다. 해당 내용을 증명하려면 고등학교 수학과정의 지식이 필요하기 때문이다. 그럼 지금부터 한번 알아보자.
| 증명하는 방법 : 구분구적법 |
해당 내용은 구분구적법을 통하여 설명할 수 있다. 구분구적법이란 도형의 넓이나 부피를 구할 대 주어진 도형을 작은 기본 도형으로 세분하여 세분된 기본 도형의 넓이나 부피의 합을 근삿값으로 구하고 이 값을 극한값으로 넓이나 부피를 구하는 방법이다.
그렇다면 이제 구분구적법을 통하여 뿔의 부피는 기둥의 부피의 3분의1임을 보여보겠다. 해당 내용은 사전 지식을 숙지하고 있음을 전제로 설명하겠다. (수열 등...)
원뿔을 예로 들어보자. 원뿔의 높이를 n등분하여 각 분점에서 밑면에 평행한 평면으로 잘라 n - 1개의 원기둥을 만들고 그 원기둥의 부피의 합을 구하면 된다.
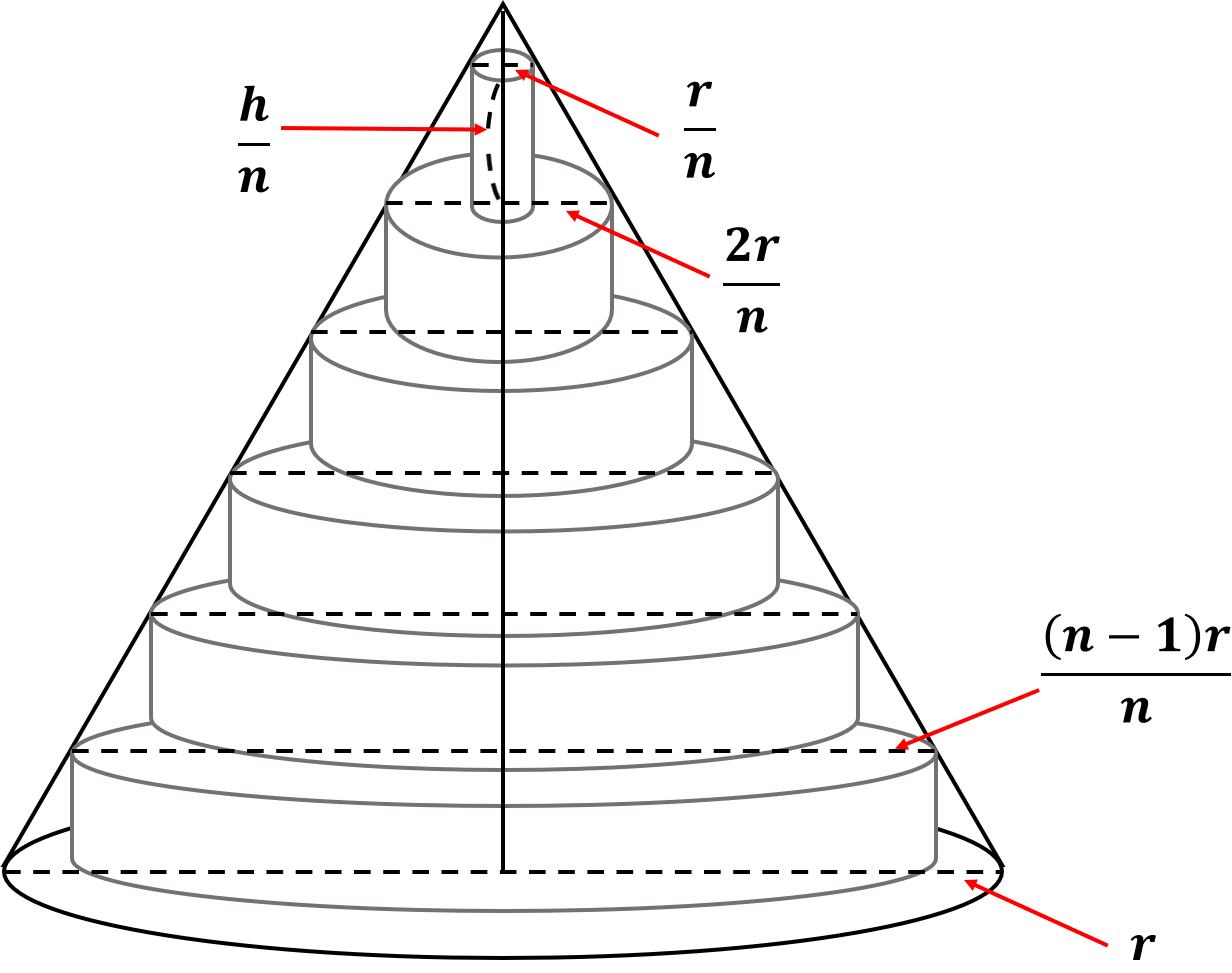
이렇게 하면 각 원기둥의 높이와 밑면의 반지름은 다음과 같이 말할 수 있다.

그럼 이제 조각난 원기둥들의 총합을 구해보자.
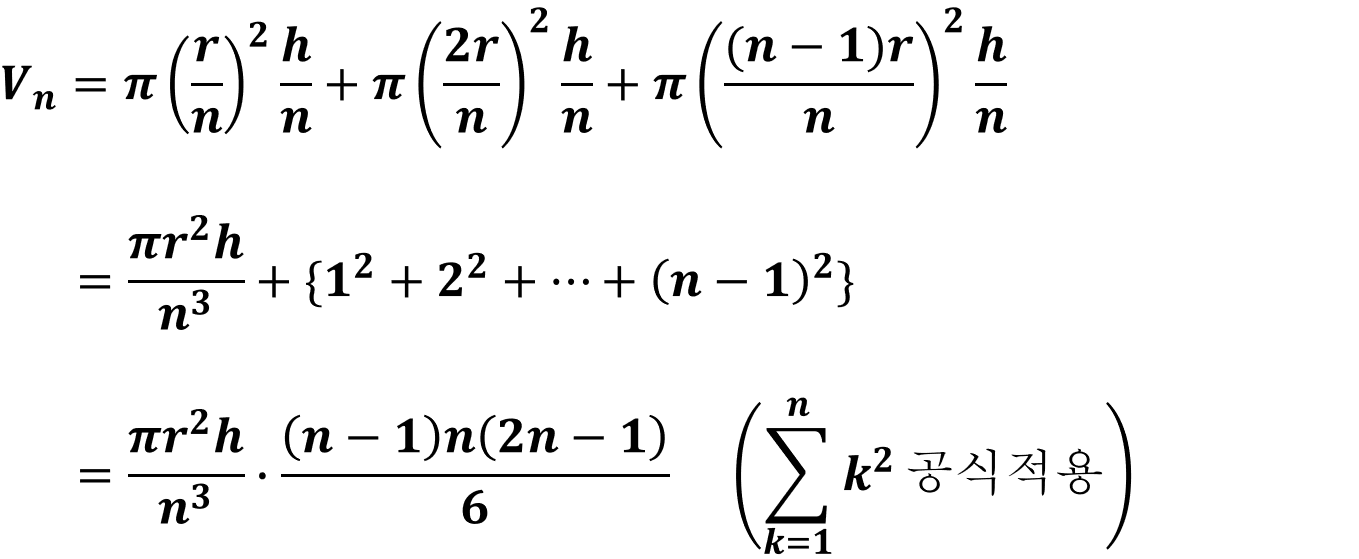
이렇게 해서 극한으로 보낼 근사값을 구하였다. 이제 이걸 극한으로 보내면 끝난다.
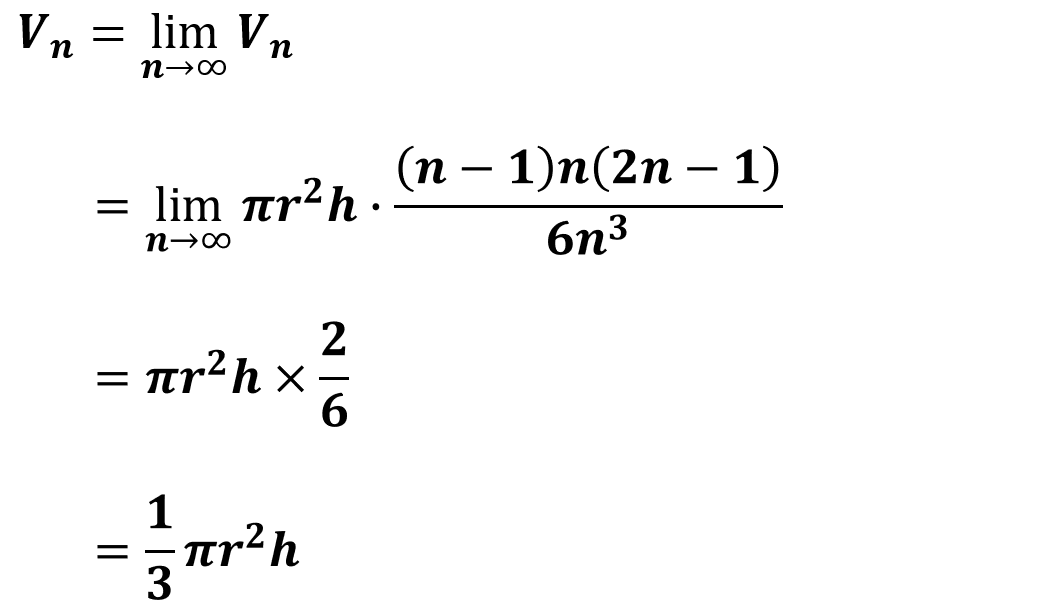
결론적으로 반지름의 길이가 r이고 높이가 h인 원뿔의 부피는 반지름의 길이가 r이고 높이가 h인 원기둥의 부피의 3분의 1이라는 것이 증명되었다. 사각뿔, 삼각뿔 등도 밑면의 모양만 다를 뿐이지 똑같은 과정으로 똑같이 증명이 된다.
※ 함께 읽기
'수학이야기 > 이론' 카테고리의 다른 글
| 원과 직선의 위치 관계 및 판별하기 (0) | 2021.11.25 |
|---|---|
| 두 직선의 위치관계 - 평행, 일치, 수직, 교차 (0) | 2021.11.22 |
| 구의 방정식에 대하여 알아보자 (0) | 2021.11.21 |
| 원의 방정식에 대하여 알아보자. (0) | 2021.11.14 |
| 직육면체의 겉넓이와 부피 구하기 (0) | 2021.11.06 |