반응형

| 위치 관계의 종류 |
두 직선이 있다면 이 둘의 위치 관계는 4가지로 구분 된다.
평행한 경우, 일치하는 경우, 수직인 경우, 만나는 경우
뭐 어떻게 그어도 이 4가지를 벗어나지 않는다. 좌표평면상에서 보면 아래와 같다.
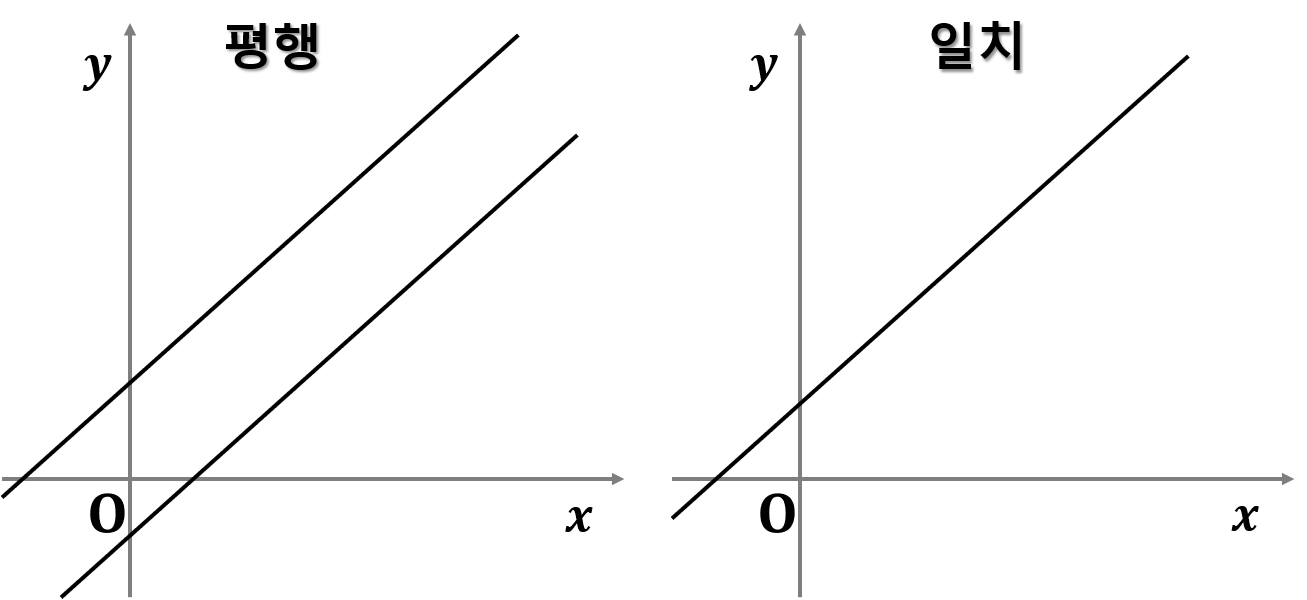

이 4가지의 위치 관계를 말로서 표현하면 아래와 같은 의미를 가진다.
| 두 직선의 평행 조건 | 두 직선의 기울기가 같고 y절편이 다르다. |
| 두 직선의 일치 조건 | 두 직선의 기울기와 y절편이 같다. |
| 두 직선의 수직 조건 | 두 직선의 기울기의 곱은 = -1 이다. |
| 두 직선이 만날 조건 | 기울기가 다르다. |
두 직선이 수직이 될 조건이 왜 기울기의 곱 = -1인지 모르겠다면 아래글을 참고하자.
두 직선이 수직일 조건과 증명하기
두 직선이 수직일 조건 임의의 두 직선이 수직이 된다면 다음과 같은 식이 성립된다. 이 조건은 상당히 많은 문제에서 응용이 되는 내용이니 잘 알고 있어야 한다. 증명하기 많은 공식이 기하학
houseofj.tistory.com
| 수식적인 표현 |
앞서 말로서 표현한 위치 관계의 의미를 식을 보고 판단을 할 줄 알아야 한다. 두 직선의 식이 주어진다면 아래와 같은 관계가 성립할 시 위치관계를 말할 수 있다. 정리하면 아래와 같다.

두 개의 직선의 방정식이 주어진다면 위와 같은 표의 내용을 활용하여 직선의 위치 관계를 알 수 있어야 한다. 기하에서 상당히 많이 활용되는 내용이니 반드시 숙지하자.
반응형
'수학이야기 > 이론' 카테고리의 다른 글
| 원의 판별식에 대하여 알아보자. (0) | 2021.11.26 |
|---|---|
| 원과 직선의 위치 관계 및 판별하기 (0) | 2021.11.25 |
| 뿔의 부피는 왜 기둥의 부피의 3분의1일까???? (0) | 2021.11.21 |
| 구의 방정식에 대하여 알아보자 (0) | 2021.11.21 |
| 원의 방정식에 대하여 알아보자. (0) | 2021.11.14 |