반응형

미지수가 x, y로 이루어진 이차식이 주어졌을 경우 이 식이 실원을 되는지 안되는지 판단할 수 있는 방법은 2가지가 있다. 이번 글에서는 실원이 되는 조건을 구하는 방법 2가지에 대하여 알아보도록 하자.
| 일반형을 표준형으로 고쳐서 실원의 조건 구하기 |
다음과 같은 이차식을 가정해보자.
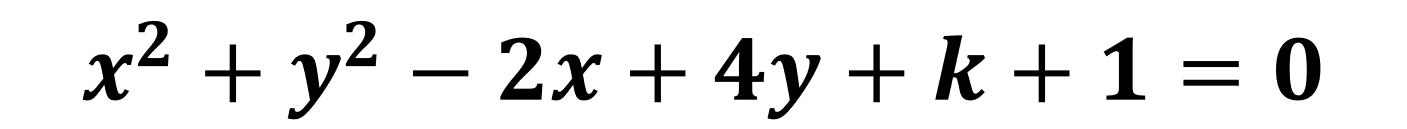
▲위 식은 원의 방정식의 일반형이다. 이것을 표준형 원의 방정식 즉, 완전제곱꼴로 고치도록 하자. 표준형으로 고쳤을 경우 반지름의 길이를 알 수 있다. 이 반지름의 길이가 0보다 크다면 실원이라 말을 할 수 있다. 이 사실을 기억하고 아래와 같이 식을 정리하자.

▲완전제곱꼴로 식을 고쳐서 문제는 푸는 방법은 가장 기본이 되는 응용 방법 중 하나다. 위와 같이 기하 관련 문제를 푸는 데도 유용하게 쓰인다.
| 원의 판별식을 이용하여 실원의 조건 구하기 |
또 다른 방법은 원의 판별식이라는 공식을 이용하는 것이다. 공식은 아주 간단하다. 만약 원의 판별식이 무엇인지 잘 모른다면 아래의 글을 읽는 것을 권장한다.
원의 판별식에 대하여 알아보자.
개요 판별식 D라는 것은 문과든 이과든 수학 공부를 하는 사람은 누구다 다 배우는 것이다. 판별식 D는 이차방정식의 해의 개수를 파악하기 위해 사용한다. 판별식 D에 관한 내용은 → 판별식 D
houseofj.tistory.com
원의 판별식을 이용하면 아래와 같이 실원의 조건을 구할 수 있다.

▲공식이긴 하지만 완전제곱꼴로 고쳐서 구하는 방법에 비하여 그리 계산이 간단하다고 할 수는 없다. 편한 방법을 골라서 문제를 풀도록 하자.

| ※ 함께 읽기 두 원의 중심거리에 따른 두 원의 위치 관계 원과 직선의 위치 관계 및 판별하기 기울기를 알 때 원의 접선의 방정식 공식 및 증명하기 두 점을 지름의 양끝으로 하는 원의 방정식 구하기 |
반응형
'수학이야기 > 이론' 카테고리의 다른 글
| 멱급수에 대하여 알아보자. (0) | 2022.11.27 |
|---|---|
| 공간에서 두 직선의 위치 관계에 대하여 알아보자 (0) | 2022.10.01 |
| 계차수열에 대하여 알아보자 (0) | 2022.09.11 |
| 원 위의 점 직선에 이르는 최소 거리와 최대 거리 구하기 (0) | 2022.08.20 |
| 지표와 가수에 대하여 알아보자 (0) | 2022.08.16 |