반응형

| 공간에서의 직선 |
공간안에는 무수히 많은 직선을 그을 수 있다. 두 개의 직선을 긋는 다면 이들의 위치 관계는 무조건 3가지 중의 하나로 분류된다. 이번 글에서는 공간에서 두 직선의 위치 관계에 대하여 알아보자.
반응형
| 위치 관계 3가지 |
하나씩 알아보도록 하자.
1. 한 점에서 만난다.

▲위의 그림 처럼 한 점에서 만나는 경우다. 이 경우 두 직선은 한 평면 위에 있다.
2. 평행.

▲평행의 의미를 모르는 사람은 없을 것이라고 생각한다. 이 역시 두 직선은 한 평면 위에 있는 것을 알 수 있다.
3. 꼬인 위치에 있는 경우.

▲세 번째로는 꼬인 위치에 있는 경우다. 한 평면 위에 있지 않은 두 직선이 만나지도 않고 평행하지도 않을 때 이 두직선은 서로 꼬인 위치에 있다고 말한다. 위 그림을 보면 직선 l과 m은 서로 만나지도 않고 평행하지도 않으며 한 평면 위에 있지 않다.
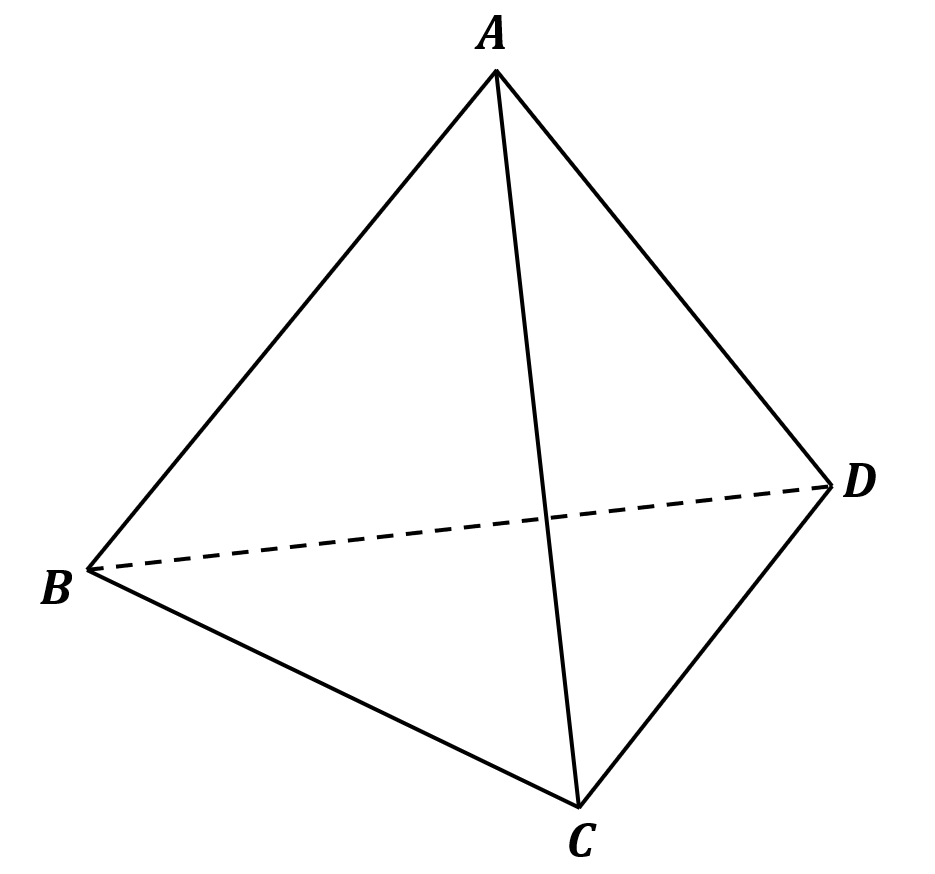
▲간단한 예시로 정사면체를 보자. 정사면체 ABCD에서 선분AB와 CD, 선분 AC와 BD, 모서리 AD와 BC를 각각 꼬인 위치에 있다고 말할 수 있다.

| ※ 함께 읽기 삼수선의 정리와 증명하는 방법 점과 직선사이의 거리 공식 및 증명하기 세 점이 일직선 위에 있을 조건 평면의 결정 조건에 대하여 알아보자. |
반응형
'수학이야기 > 이론' 카테고리의 다른 글
| 삼각함수의 값의 부호 정리 (1) | 2022.11.29 |
|---|---|
| 멱급수에 대하여 알아보자. (0) | 2022.11.27 |
| 실원이 되기 위한 조건에 대하여 알아보자. (0) | 2022.09.27 |
| 계차수열에 대하여 알아보자 (0) | 2022.09.11 |
| 원 위의 점 직선에 이르는 최소 거리와 최대 거리 구하기 (0) | 2022.08.20 |