
| 모든 수학문제는 개념의 응용 |
수학 문제를 풀 때 항상 강조되는 문장이 있다. 개념이 가장 중요하다. 정말 백번 맞는 말이다. 결국 우리가 교육과정에서 접하는 모든 수학 문제는 개념의 응용이다. 변별력을 더한다면 개념의 응용에서 한 발자국 더 나아가 그 개념을 토대로 창의적인 사고를 요구한다.
원 위의 점에서 직선까지의 최소, 최대 거리를 구하는 것이 바로 좋은 예라고 생각한다. 이 문제는 개념의 응용과 창의적인 사고를 동시에 요구하는 문제다. 요구를 할 뿐이지 사실 굉장히 기본적인 수준의 문제다. 어떻게 풀 것인가? 단계적으로 생각해보자.
| 구하는 방법 |

▲위에 보이는 것과 같이 원과 직선이 있다. 직선의 방정식과 원의 방정식이 주어진다면 여기서 알 수 있는 것은 무엇일까? 당연히 반지름의 길이를 알 수 있고, 점과 직선 사이의 거리 공식을 사용하여 원의 중심점과 직선의 거리를 알 수 있다. 그러면 여기서 수직으로 선을 쭉 그어보자.

▲선을 원 끝까지 쭉 그어보자. 그러면 그림을 통하여 직관적으로 알 수 있다. 원 위의 점에서 직선에 이르는 최소 거리는 원의 중심과 직선의 거리에서 원의 반지름 만큼이 빠진 값이고 최대 거리는 원의 반지름만큼 더해진 값이라는 것을. 정리하면 아래와 같다.

| 예제 |
아래와 같이 원의 방정식과 직선의 방정식이 주어졌다고 생각해보자.
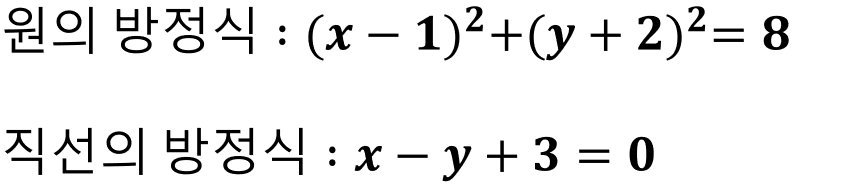
▲원의 방정식을 통하여 원의 중심점의 좌표가 (1, -2), 반지름의 길이가 2√2이라는 것을 알 수 있다. 직선의 방정식도 제시되어 있으니 점과 직선사이의 거리 공식을 사용하여 원의 중심과 직선 사이의 거리를 구하자. 공식을 모르겠다면 아래의 글을 참고하도록 하자.
점과 직선사이의 거리 공식 및 증명하기
점과 직선 사이의 거리 공식 점 P(x₁, y₁)에서 직선 ax+by+c=0까지의 거리를 d라고 둔다면 d는 다음과 같은 공식으로 구할 수 있다. 거의 뭐 구구단처럼 많이 쓰이는 공식이니 꼭 알아둬야한다. 참
houseofj.tistory.com
원의 중심과 직선사이의 거리를 d라고 하면, 공식을 사용하여 아래와 같이 구할 수 있다.
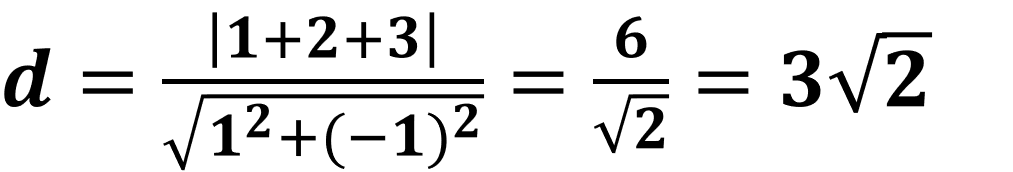
▲이제 반지름의 길이도 알고 있으니 최대, 최소 거리를 구하는 것은 끝난 것이나 다름없다. 최종적으로 정리해보자.
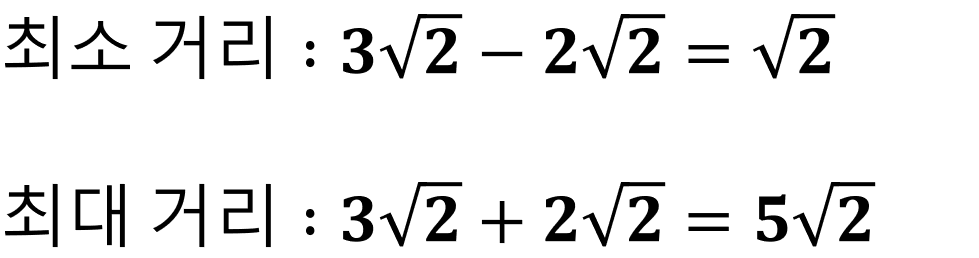
▲이렇듯 간단한 응용으로 문제가 풀렸다. 비록 이 문제는 아주 쉬운 문제이지만, 많은 어려운 문제도 응용을 잘하면 정말 간단하게 풀리는 경우가 상당히 많다. 수학적인 사고력을 기를 수 있도록 하자.

| ※ 함께 읽기 점과 직선사이의 거리 공식 및 증명하기 두 원의 중심거리에 따른 두 원의 위치 관계 원의 둘레(원주)와 원의 넓이 구하기 기울기를 알 때 원의 접선의 방정식 공식 및 증명하기 |
'수학이야기 > 이론' 카테고리의 다른 글
| 실원이 되기 위한 조건에 대하여 알아보자. (0) | 2022.09.27 |
|---|---|
| 계차수열에 대하여 알아보자 (0) | 2022.09.11 |
| 지표와 가수에 대하여 알아보자 (0) | 2022.08.16 |
| 상용로그와 상용로그표 읽는 법 (0) | 2022.08.14 |
| 삼차방정식 근과 계수의 관계 (0) | 2022.08.07 |