반응형

| 등비수열의 합 공식 |
등비수열이 수열에서 가장 많이 접하게 되듯이 등비수열의 합 공식 또한 많이 접하게 되는 공식 중 하나다.
등비수열의 첫째항을 a, 공비를 r이라고 하면, 첫째항부터 n항까지의 합 Sn은 다음과 같이 말할 수 있다.
참고로 등비수열의 합은 2가지 경우가 있다.
첫째는 공비가 1이 아닐 때
둘째는 공비가 1일 때
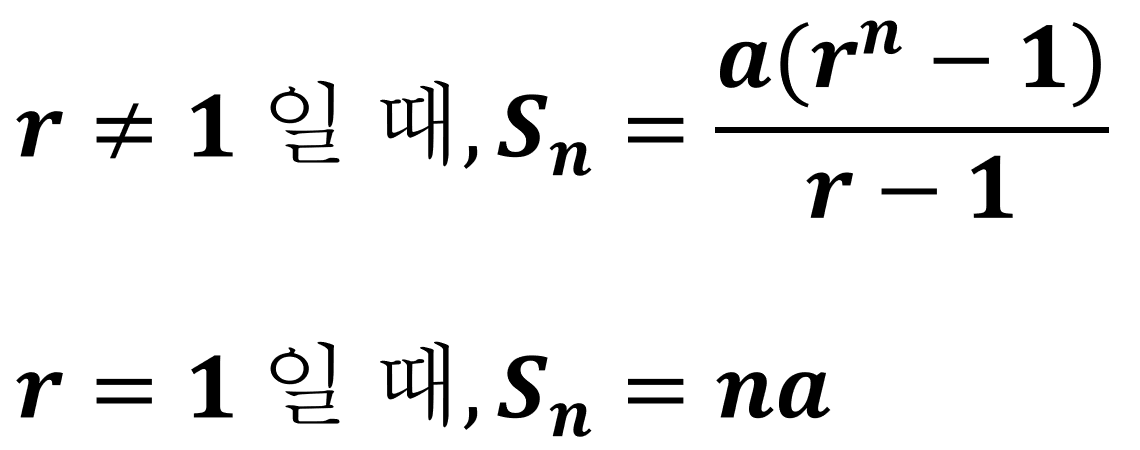
| 증명하기 |
등비수열의 합의 공식을 유도하는 것은 등차수열의 합의 공식을 유도하는 것과 비슷하지만 미묘한 차이가 있다.
기존의 Sn을 나열한 식과 이 식에 r을 곱한 식을 나열하여 연산하면 쉽게 유도할 수 있다.
아래를 보자.
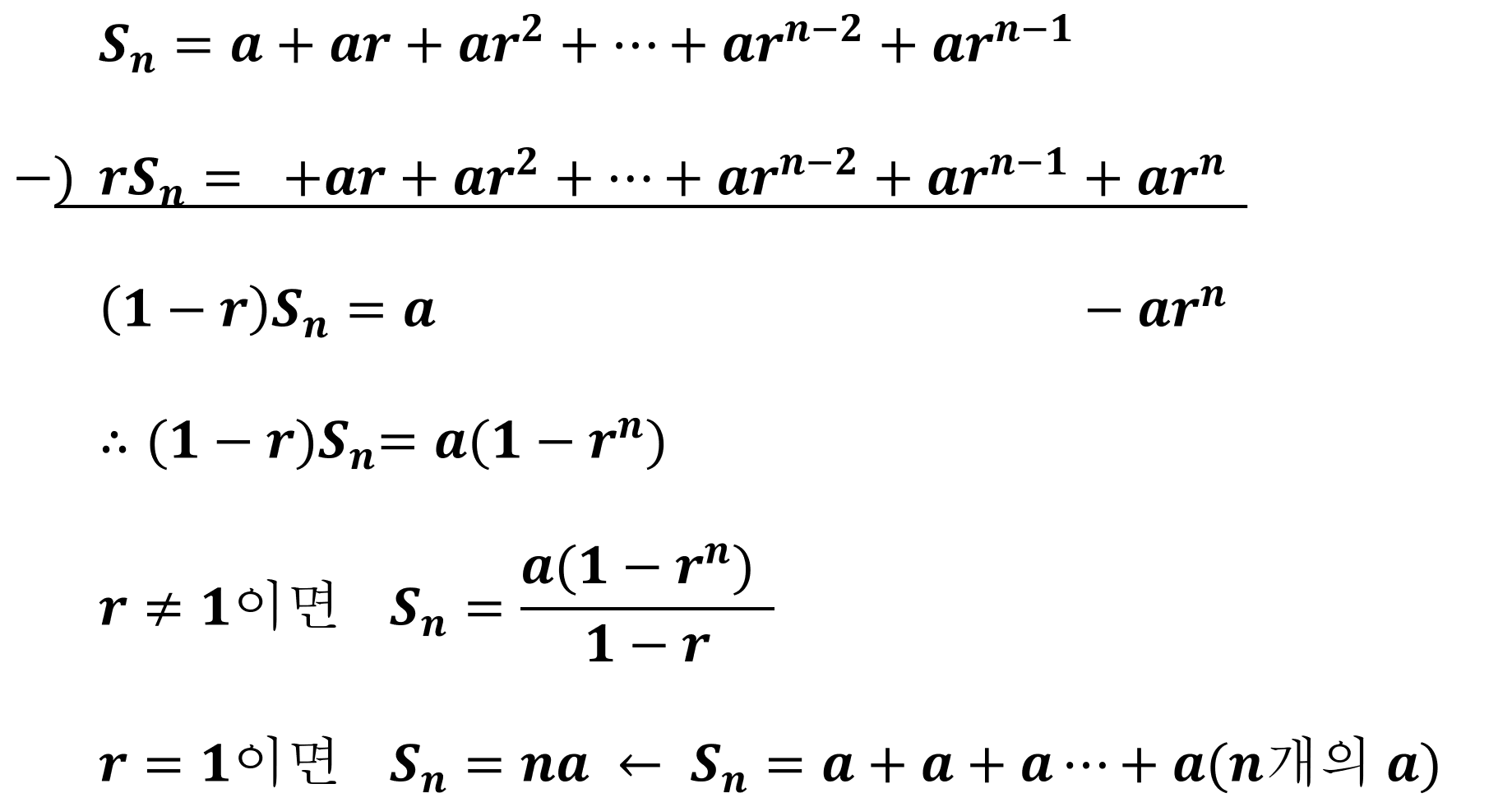
| 등비수열의 합의 공식으로 일반항 구하기 |
등차수열의 합의 공식으로 일반항을 구하는 것과 전혀 다르지 않다.
Sn-1에 an이 더해진 것이 Sn이다.
즉.
Sn = a1+a2+a3+.....+an-1+an
Sn-1 = a1+a2+a3+.....+an-1
두 식을 뺀다면 결국 Sn-Sn-1 = an 일반항을 구할 수 있다.
※함께 읽기
등비수열과 등비수열의 일반항, 등비중항
등비수열이란? 첫째항부터 차례로 일정한 수를 곱해서 얻어지는 수열을 등비수열이라고 하며, 여기서 일정한 수를 공비라고 표현한다. 간단한 예를 들면 1, 2, 4, 8, 16.....이런식으로 나열이 되
houseofj.tistory.com
반응형
'수학이야기 > 이론' 카테고리의 다른 글
| 모든 수에 0을 곱하면 0이 되는 이유 (0) | 2022.04.20 |
|---|---|
| 두 원의 중심거리에 따른 두 원의 위치 관계 (0) | 2021.12.05 |
| 등차수열 합의 공식과 증명 및 일반항 구하기 (0) | 2021.11.30 |
| 등차수열과 등차수열의 일반항, 등차중항 (0) | 2021.11.29 |
| 원의 판별식에 대하여 알아보자. (0) | 2021.11.26 |