
| 수열이란? |
수열이란 어떤 일정한 규칙에 따라 차례로 나열된 수의 열을 말하며 수열의 각 수를 그 수열의 항이라고 한다. 예를 들면 수열을 a₁, a₂, a₃....으로 나열되어 있을 때 a₁을 첫째항, a₂을 둘째항이라고 한다. 그리고 여기서 n번째 항 an을 일반항이라고 말한다. 그럼 이제 이 글의 메인인 등차수열에 대하여 알아보도록 하겠다.
| 등차수열이란? |
첫째항부터 차례로 일정한 수를 더해서 얻어지는 수열을 등차수열이라고 하며, 여기서 일정한 수를 공차라고 표현한다.
무슨 소리냐면
예를 들어 아래와 같이 1, 4, 7, 10, 13..... 과 같은 수열이 있다고 하자.

| 등차수열의 일반항 |
위와 같은 등차수열의 경우 항의 개수가 무한히 많다. 따라서 나열한다면 지구 한 바퀴를 돌아도 부족한 수준이다. 이 긴걸 하나하나 나열하여 쓸 수는 없다. 따라서 수열은 일반항이라고 부르는 식으로 표현한다.
다시 수열 1, 4, 7, 10 ,13..... 을 예로 들어보자.
여기서 첫째항은 1이다.
둘째항은 첫째항에 공차 3을 더한 값인 4
셋째항은 첫째항에 공차 3을 2번 더한 값인 7
넷째항은 첫째항에 공차 3을 3번 더한 값인 10.....
정리하면 n번째 항은 첫째항에 공차 3을 n -1번째 더한 값이 된다.
즉, 등차수열의 일반항, 즉 n번째항은 첫째항에 공차 d를 n -1 번 더한 식이다.

| 등차중항이란? |
세 수 a, b, c가 이 순으로 등차수열을 이룰 때 b를 a, c의 등차중항이라고 한다.
이경우 아래와 같은 식이 성립된다.

증명하는 방법은 아주 간단하다. 그냥 일반항을 넣어서 정리하면 끝난다.
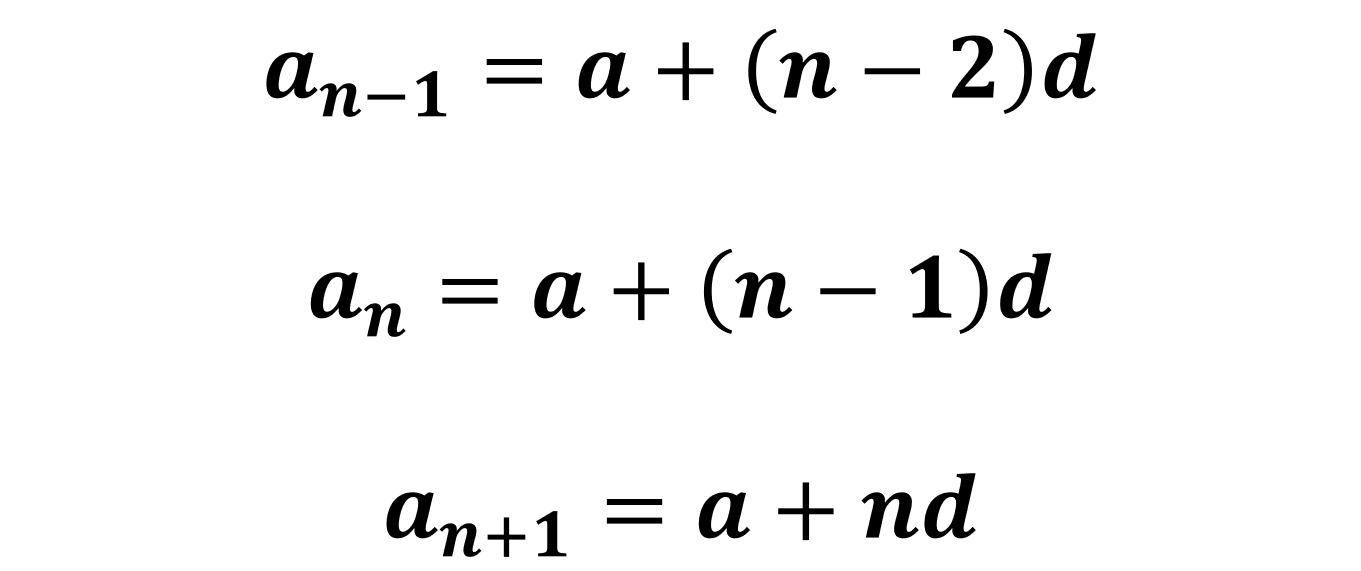
이렇게 나란히 3개의 항을 쓰고 대입하여보자.
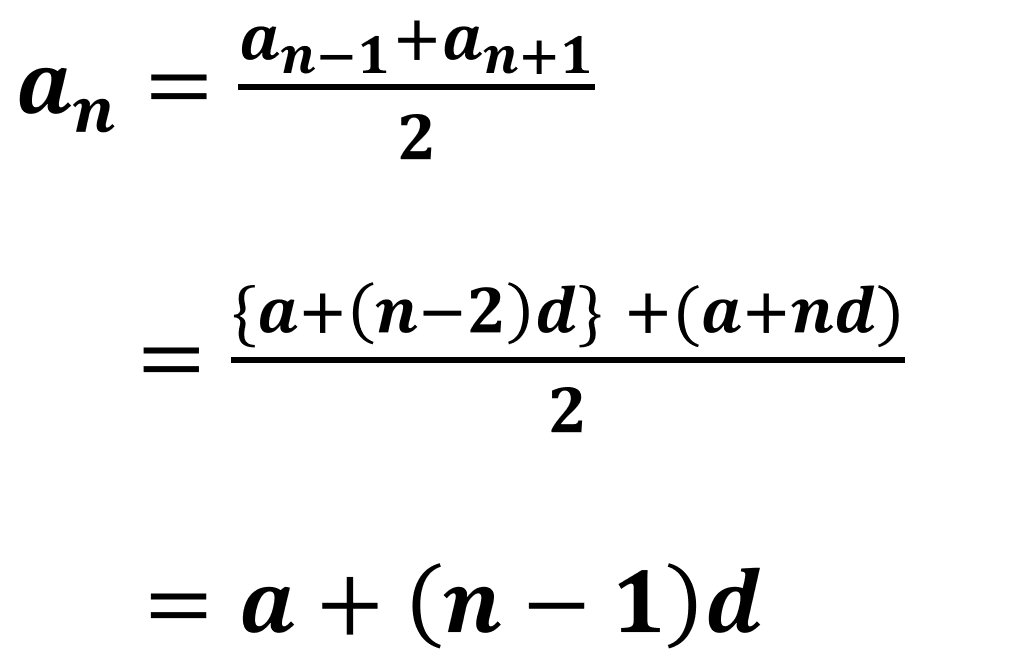
이렇게 쉽게 정리할 수 있다. 등차수열은 쉬운 내용이지만 개념을 정확하게 알고 있어야 한다. 사실 모든 수학에 해당되는 내용이긴 하지만..
'수학이야기 > 이론' 카테고리의 다른 글
| 등비수열의 합 공식 및 증명하기 (0) | 2021.12.04 |
|---|---|
| 등차수열 합의 공식과 증명 및 일반항 구하기 (0) | 2021.11.30 |
| 원의 판별식에 대하여 알아보자. (0) | 2021.11.26 |
| 원과 직선의 위치 관계 및 판별하기 (0) | 2021.11.25 |
| 두 직선의 위치관계 - 평행, 일치, 수직, 교차 (0) | 2021.11.22 |