
| 삼각함수 관련 공식의 특징 |
삼각함수에는 여러 가지 공식이 있다. 거의 뭐 대부분의 공식이 복잡한 계산을 간단하게 하기 위해 존재하듯, 삼각함수 관련 공식 또한 그러한 목적으로 존재한다. 차이점이 있다면 삼각함수 관련 공식은 눈에 잘 들어오지 않는다는 것이다. 그 이유는 학교에서 삼각함수라는 개념을 접하는 시점이 그리 어린 나이가 아니기 때문에 우리에게 익숙하지 않기 때문이다. 따라서 삼각함수 관련 공식은 무조건 철저하게 외워야 한다. 이번 글에서는 삼각함수 관련 공식 중 하나인 배각의 공식에 대하여 알아보도록 하자.
| 배각 공식 |
배각 공식은 sin, cos, tan마다 하나씩 총 3가지가 있다.

▲복잡한 삼각함수 관련 식 가운데서도 배각 공식은 그나마 외우기가 쉬운 공식이다. 정말 구구단처럼 쓰이는 식들이니 반드시 외우도록 하자.
| 증명하는 방법 |
배각 공식을 증명하기 위해 알아야 하는 것이 있다. 바로 삼각함수의 덧셈 정리다. 배각 공식의 증명과정은 삼각함수의 덧셈 정리의 응용이다. 아니, 정확하게 말하면 삼각함수 덧셈 정리 그 자체다. 삼각함수의 덧셈 정리에 대하여 잘 모른다면 아래의 글을 읽도록 하자. ▼
삼각함수의 덧셈정리와 증명하기
삼각함수의 덧셈정리란? 삼각함수의 덧셈정리... 상당히 많이 활용되는 공식이다. sin, cos, tan에 대하여 아래와 같이 말할 수 있다. 이때 α, β는 주어진 식의 각을 분해하여 특수각으로 나타낸다.
houseofj.tistory.com
sin 2𝛂 의 경우
sin에 관련된 덧셈 공식을 활용하여 증명할 수 있다.▼

cos 2𝛂의 경우
마찬가지로 cos에 관련된 덧셈 공식으로 증명할 수 있다.▼

tan 2𝛂의 경우
sin, cos과 전혀 다를 것 없다. 이 역시 tan에 관련된 덧셈 공식으로 증명할 수 있다.▼
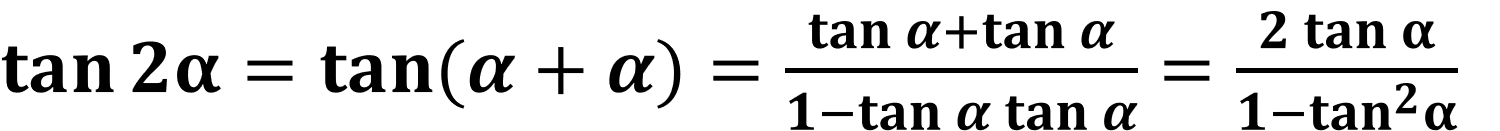

| ※ 함께 읽기 삼각함수 3배각의 공식 및 증명하기 삼각함수의 그래프에 대하여 알아보자.(sin,cos,tan) 삼각함수의 변환 공식에 대하여 알아보자. 제1코사인법칙 및 유도과정에 대하여 알아보자 |
'수학이야기 > 공식 모음' 카테고리의 다른 글
| 삼각함수 제곱 공식 및 증명하기 (0) | 2023.03.18 |
|---|---|
| 삼각함수 반각 공식 및 증명하기 (0) | 2023.03.12 |
| 삼각함수 3배각의 공식 및 증명하기 (0) | 2023.03.03 |
| 분수함수의 역함수 공식 및 증명하기 (0) | 2023.02.16 |
| 산술평균, 기하평균, 조화평균 증명하기 (0) | 2023.01.29 |