반응형

| 삼각형의 무게중심 공식 |
삼각형의 무게중심의 정의는 간단명료하게 말하자면 삼각형의 세 중선의 교점을 말한다. 무게중심의 핵심적인 성질은 각 중선을 꼭지점으로부터 2 : 1로 내분한다는 것이다. 삼각형의 세 점을 A(x₁, y₁), B(x₂, y₂), C(x₃, y₃)라고 한다면 삼각형 ABC의 무게중심 G의 좌표를 아래와 같이 표현을 할 수 있다.


▲공식은 굉장히 쉽고 간단하다. 암기 난이도는 한 번만 스쳐가듯이 봐도 기억을 할 수 있는 정도다. 이번에는 이 공식이 과연 어떻게 나오는 것인지 증명을 해보도록 하자.
반응형
| 무게중심 증명하는 방법 |
증명하는 방법은 어렵지는 않으나 이래저래 귀찮은 계산이 좀 있다. 그러니 그냥 이런 거구나 정도로 생각하도록 하자.
삼각형의 세 점을 A(x₁,y₁), B(x₂, y₂), C(x₃, y₃)이라 두고 무게중심을 G(x, y), 선분 BC의 중점을 M(x', y')라 두면 아래와 같은 그림으로 나타낼 수 있다.

▲점 M은 선분 BC의 중점이기 때문에 점 M은 아래와 같이 표현을 할 수 있다.
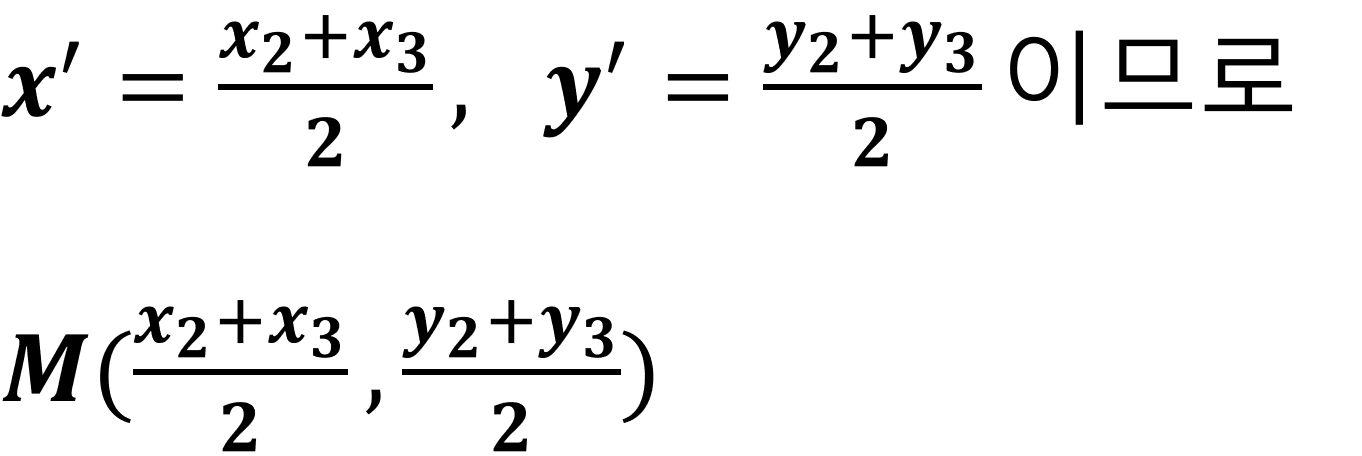
▲그리고 무게중심 G(x,y)는 중선 AM을 2 : 1로 내분하는 점이다. 점 A의 좌표와 점 M의 좌표를 알고 있으니 아래와 같이 정리하여 결론을 낼 수 있다.
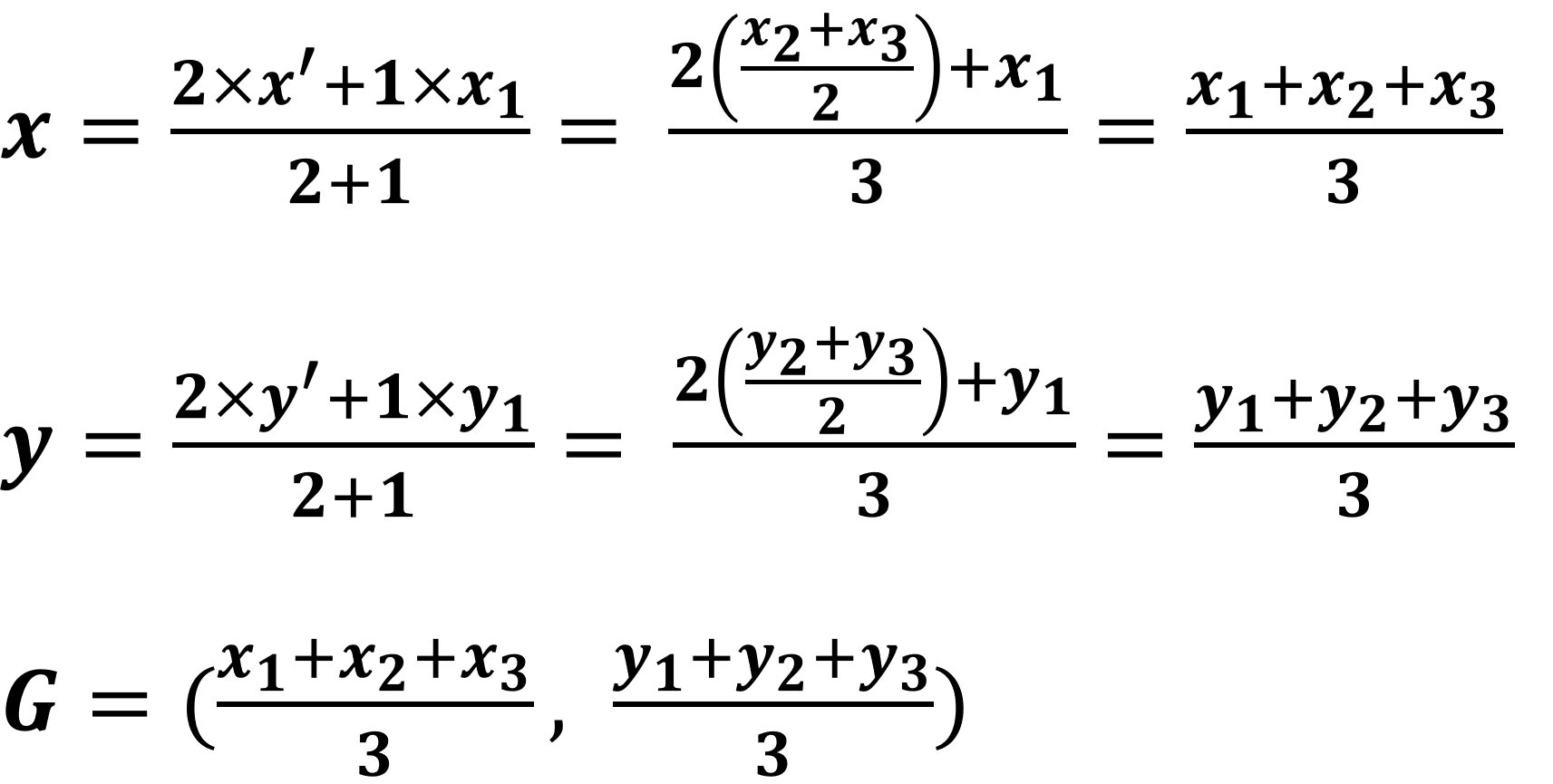
▲이렇게 무게중심의 공식을 증명할 수 있다. 증명에 들어간 개념은 아주 기초적인 수준이다. 다만 앞서 말한 것처럼 계산과정이 다소 귀찮은 편이니 공식을 필히 암기하도록 하자.

| ※ 함께 읽기 선분의 내분점과 외분점 공식 및 증명하기 두 직선이 수직일 조건과 증명하기 이등변삼각형 넓이 공식 및 유도 두 직선의 위치관계 - 평행, 일치, 수직, 교차 |
반응형
'수학이야기 > 공식 모음' 카테고리의 다른 글
| 코시-슈바르츠 부등식 증명하기 (0) | 2023.01.28 |
|---|---|
| 두 구가 내접할 조건에 대하여 알아보자. (0) | 2022.10.03 |
| 기울기를 알 때 원의 접선의 방정식 공식 및 증명하기 (0) | 2022.08.09 |
| 정십이각형 넓이 공식 및 증명하기 (0) | 2022.07.13 |
| 로그의 밑변환 공식 및 증명하기 (0) | 2022.06.26 |