반응형

| 내분점과 외분점 공식 |
수직선 위의 두 점 A(x₁), B(x₂)를 잇는 선분 AB를 m:n으로 내분하는 점을 P, 외분하는 점을 Q라 하면 내분점과 외분점을 다음과 같은 공식으로 나타낼 수 있다.


▲기하 공부에 있어서 가장 기초적인 공식 중 하나이며, 구구단처럼 필수적인 내용이라고 말을 할 수 있다.
| 내분점의 공식 증명하는 방법 |
증명하는 것은 그리 어렵지 않다. 선분 AB를 m:n으로 내분한다는 것을 아래와 같이 그릴 수 있다.▼

위 그림을 보면 한 가지 관계식을 만들어 낼 수 있다. 정확하게 비례식을 만들 수 있다.▼

위의 비례식을 x에 대하여 정리해보자.▼

▲생각보다 쉽게 내분점의 공식을 구할 수 있다.
| 외분점의 공식 증명하는 방법 |
외분점의 공식 증명하는 방법도 내분점과 크게 다르지 않다. 다만 외분점은 2가지 경우를 생각할 수 있으며 도출되는 공식은 같다. m > n 경우를 살펴보자.▼

마찬가지로 위 그림으로 비례식을 세울 수 있다.▼
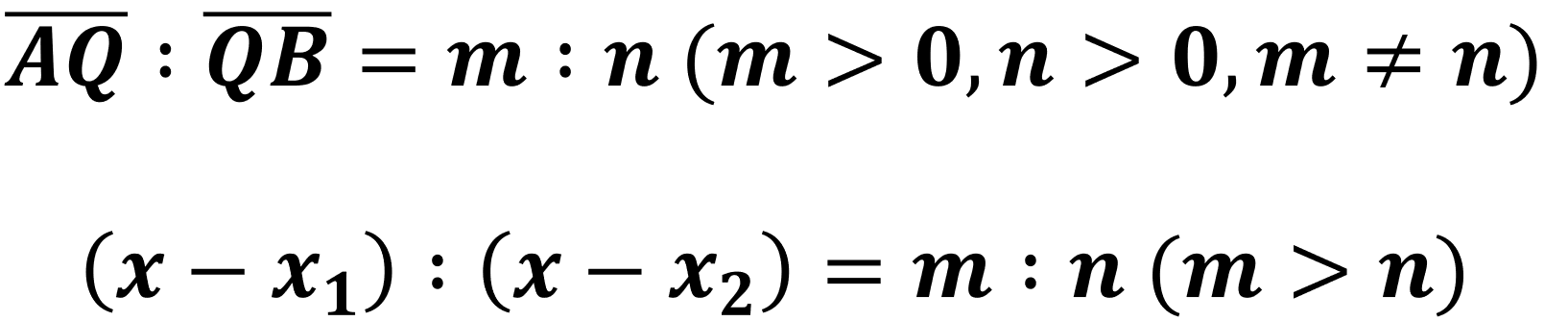
이제 위 식을 x로 정리하면 된다.▼
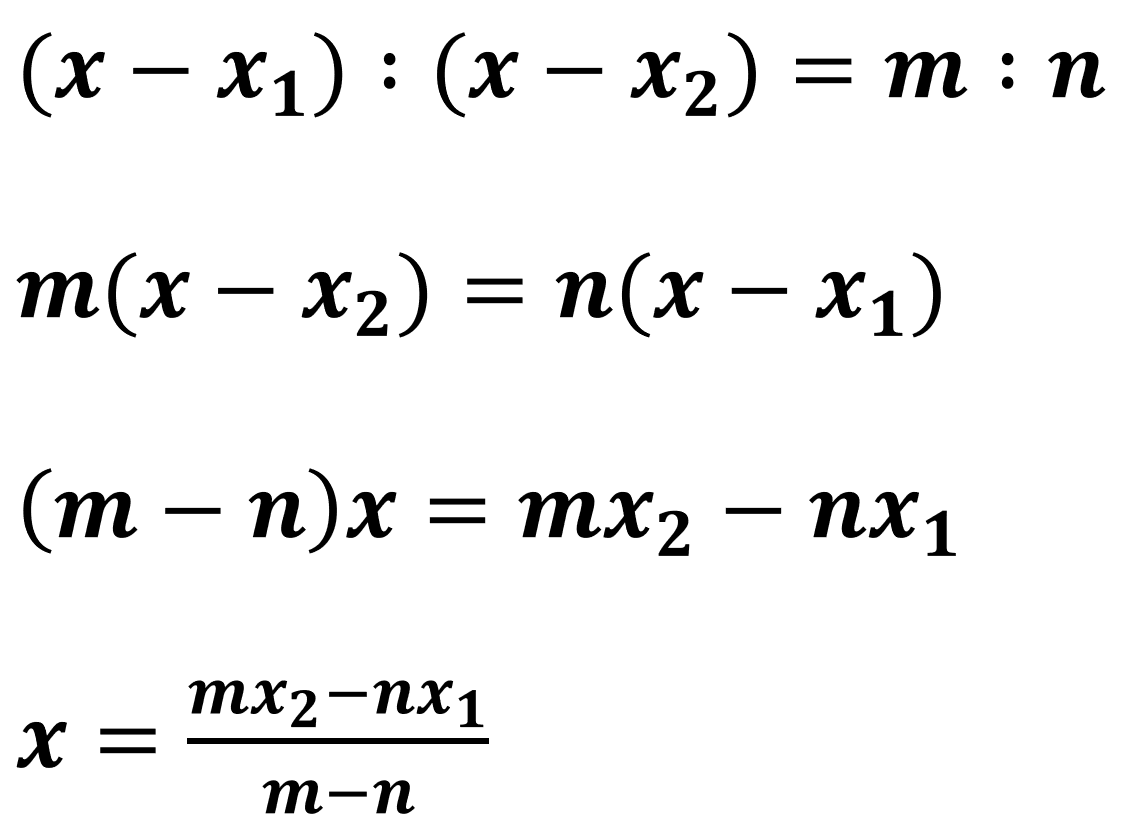
반응형
이번에는 m < n일 경우를 보자.▼

역시 아까와 마찬가지로 위 그림을 통하여 비례식을 세우자.▼
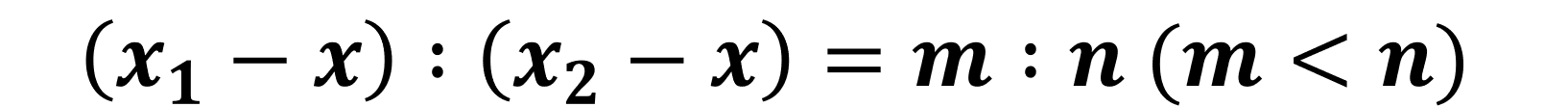
이제 위 식을 x로 정리하면 된다.▼
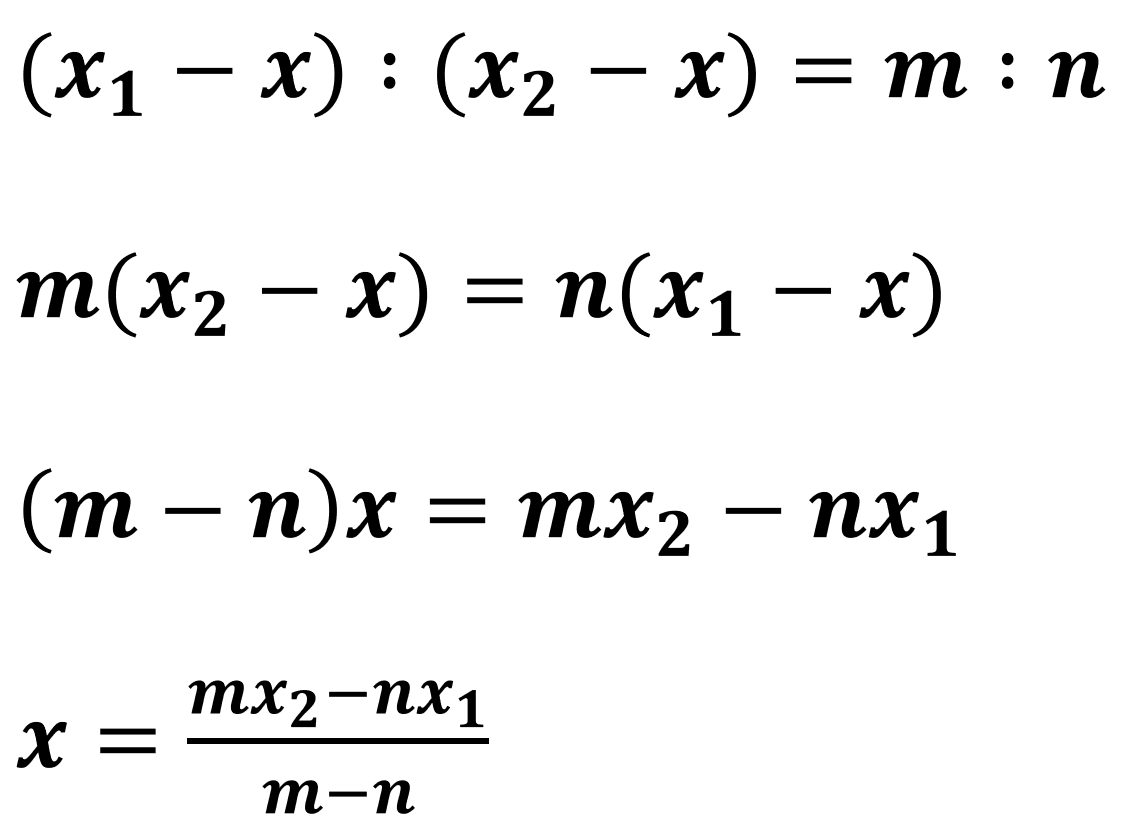
이렇든 선분의 내분점과 외분점 공식을 증명하는 것은 상당히 단순한 내용이다. 하지만 문제를 풀 때마다 매번 공식을 유도해서 푼다는 것은 어리석은 일이다. 반드시 외우도록 하자.

| ※ 함께 읽기 평행한 두 직선 사이의 거리 구하기 점의 대칭이동 하는 방법 두 직선이 이루는 각의 이등분선 방정식 구하기 두 직선의 위치관계 - 평행, 일치, 수직, 교차 |
반응형
'수학이야기' 카테고리의 다른 글
| 포물선과 직선의 위치 관계 (0) | 2023.03.31 |
|---|---|
| 방정식의 부정과 불능 (0) | 2023.02.15 |