
| 두 직선이 만나서 이루는 각 |
두 직선이 만나면 서로 다른 크기의 각이 2개씩 만들어진다. 수직으로 만난다면 같은 크기의 각 4개가 될 것이다.
계산기 프로그램을 사용하여 2개의 직선을 그려보자. 컴퓨터로 그래프를 그리는 방법은 여러 가지가 있지만 어지간한 그래프는 윈도우에서 기본적으로 제공하는 계산기로 다 그릴 수 있으니 잘 활용하도록 하자. 계산기로 그래프 그리는 방법은 아래의 글을 참고하자.
[Window10] 윈도우10 계산기로 그래프 그리는 방법
윈도우10 계산기의 기능 윈도우10에는 기본 보조프로그램으로 계산기가 설치되어 있다. 보통 암산으로 해결하기에는 좀 껄끄러운 계산을 할 때 주로 사용할 것이다. 계산기는 절대 실수를 하지
houseofj.tistory.com

▲위와 같이 2개의 직선을 그으면 직선이 평행하지 않는 이상 무조건 4개의 각이 만들어진다. 앞서 언급했지만 일반적으로 서로 다른 크기의 각 2개가 만들어지지만 위와 같은 경우는 기울기가 수직을 이루기 때문이 직각이 4개가 만들어진다. 이번 글에서는 두 직선이 이루는 각의 이등분선 방정식을 구하는 방법에 대하여 알아보자.
| 각의 이등분선 방정식 구하기 |
대부분의 기하학 문제가 그렇지만 이 경우에도 결국 기본 개념을 응용하는 과정이다. 각의 이등분선 위의 임의의 점에서 두 직선에 이르는 거리는 같다. 따라서 임의의 점을 P(x, y)로 두고 점과 직선사이의 거리 공식을 적용하면 쉽게 구할 수 있다.
점과 직선사이의 거리 공식을 모르겠다면 아래의 글을 참고하자.
점과 직선사이의 거리 공식 및 증명하기
점과 직선 사이의 거리 공식 점 P(x₁, y₁)에서 직선 ax+by+c=0까지의 거리를 d라고 둔다면 d는 다음과 같은 공식으로 구할 수 있다. 거의 뭐 구구단처럼 많이 쓰이는 공식이니 꼭 알아둬야한다. 참
houseofj.tistory.com
임의의 점 P(x, y)와 두 직선 2x - y -1 = 0, x + 2y - 1 = 0 이 있으므로 점과 직선사이의 거리 공식을 적용하자.▼

▲위와 같이 각의 이등분선 방정식은 2개나 나온다. 이것을 좌표평면에 그려보면 확연하게 알 수 있다.
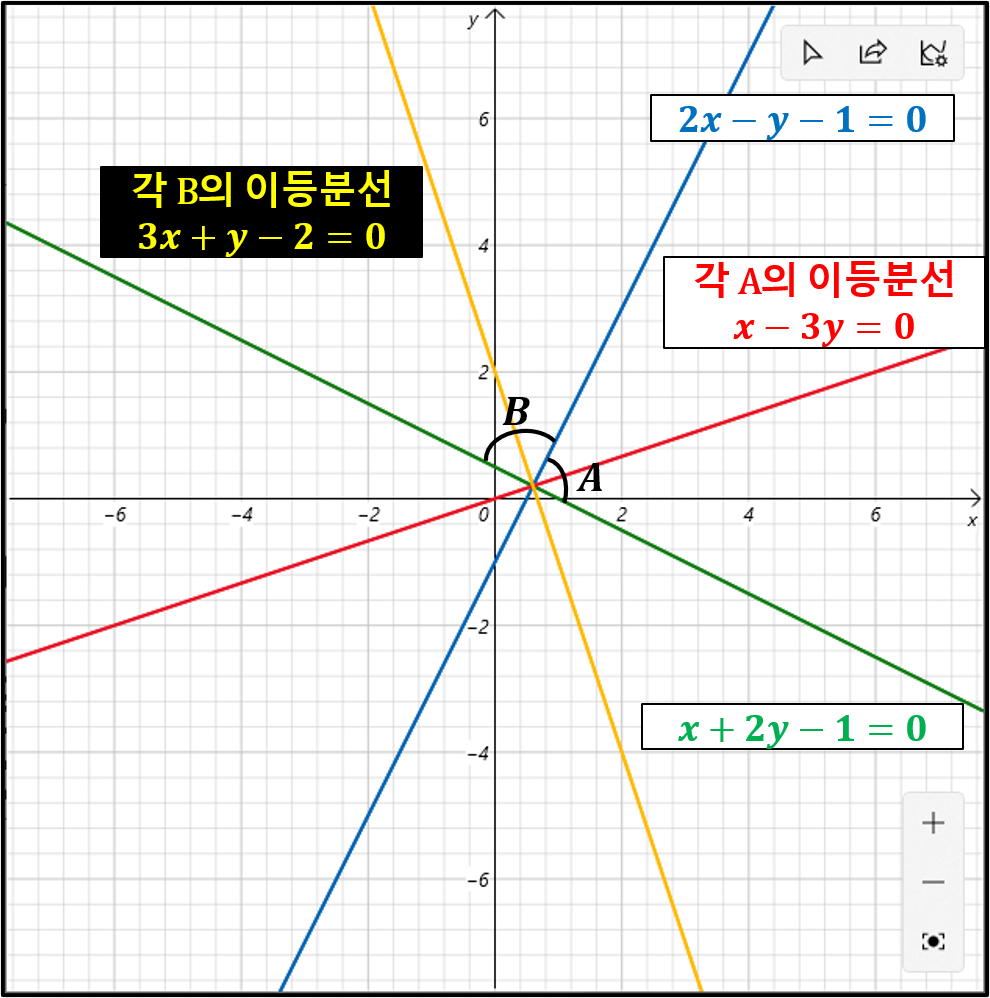
▲한 직선은 두 직선이 이루는 각 A를 이등분하고 나머지 하나는 각 B를 이등분한다. 이등분선 방정식 자체를 구하라는 문제는 나오지 않을 것이다. 하지만 이 사실을 응용하는 문제는 얼마든지 나올 수 있으니 필수로 익히도록 하자.

| ※ 함께 읽기 세 점이 일직선 위에 있을 조건 점의 대칭이동 하는 방법 두 직선이 수직일 조건과 증명하기 직선의 방정식 공식 및 증명하기 |
'수학이야기 > 이론' 카테고리의 다른 글
| 상용로그와 상용로그표 읽는 법 (0) | 2022.08.14 |
|---|---|
| 삼차방정식 근과 계수의 관계 (0) | 2022.08.07 |
| 점의 대칭이동 하는 방법 (0) | 2022.08.05 |
| 평행한 두 직선 사이의 거리 구하기 (4) | 2022.07.31 |
| 두 점을 지름의 양끝으로 하는 원의 방정식 구하기 (0) | 2022.07.22 |