반응형

| 산술평균, 기하평균, 조화평균 |
산술평균, 기하평균, 조화평균. 이 셋은 유명한 절대부등식으로써 수포자가 아니라면 정말 많이 들어본 단어일 것이고 또 그만큼 많이 쓰이는 내용이다. 절대부등식이니 당연히 부등식 관련 문제에서 많이 나오며, 두 수의 합이나 곱의 최댓값, 최솟값 등을 구하는 경우 많이 쓰인다. 식은 다음과 같다.

▲필자가 한창 수학 공부를 하던 시절에는 조화평균은 거의 접한 적이 없었다. 그렇다고 숙지를 안한건 아니었다. 산술평균과 기하평균은 지겹게 봤을 것이다. 저게 왜 성립을 할 수 있을까? 증명을 해보자.
반응형
| 증명하기 |
굉장히 많이 나오는 내용이라 뭔가 증명하는 방법도 화려할 것 같은 느낌이 들지만 의외로 간단한 사칙연산을 통하여 손쉽게 증명이 가능하다.

▲위와 같이 식 ①, ②같은 관계를 알아냈다. 이들을 하나로 정리하면 우리가 잘 알고 있는 산술평균, 기하평균, 조화평균의 관계가 만들어진다.
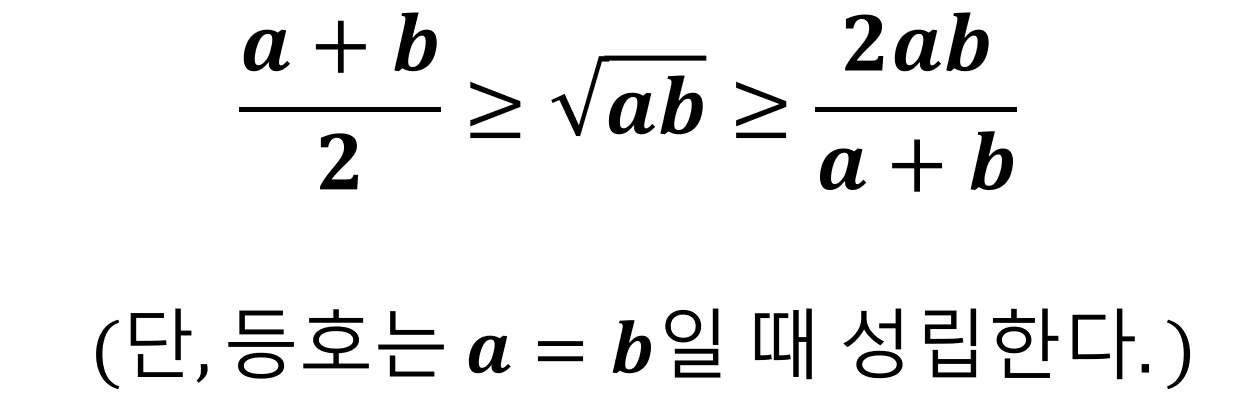
▲바로 이렇게 말이다. 상당히 중요한 내용으로 통암기는 기본이고, 그렇게 어려운 내용은 아니니 증명과정도 숙지하는 것을 권장한다. 굉장히 많이 응용이 되는 내용이기 때문이다.

| ※ 함께 읽기 코시-슈바르츠 부등식 증명하기 실수의 대소에 대한 기본 성질 및 증명하기 |
반응형
'수학이야기 > 공식 모음' 카테고리의 다른 글
| 삼각함수 3배각의 공식 및 증명하기 (0) | 2023.03.03 |
|---|---|
| 분수함수의 역함수 공식 및 증명하기 (0) | 2023.02.16 |
| 코시-슈바르츠 부등식 증명하기 (0) | 2023.01.28 |
| 두 구가 내접할 조건에 대하여 알아보자. (0) | 2022.10.03 |
| 삼각형의 무게중심 공식 및 증명하기 (0) | 2022.09.10 |