반응형

| 두 직선이 수직일 조건 |
임의의 두 직선이 수직이 된다면 다음과 같은 식이 성립된다.

이 조건은 상당히 많은 문제에서 응용이 되는 내용이니 잘 알고 있어야 한다.
| 증명하기 |
많은 공식이 기하학적으로 접근하면 쉽게 증명할 수 있는 경우가 많다. 이 내용도 그러하다.
아래의 그림을 보자.
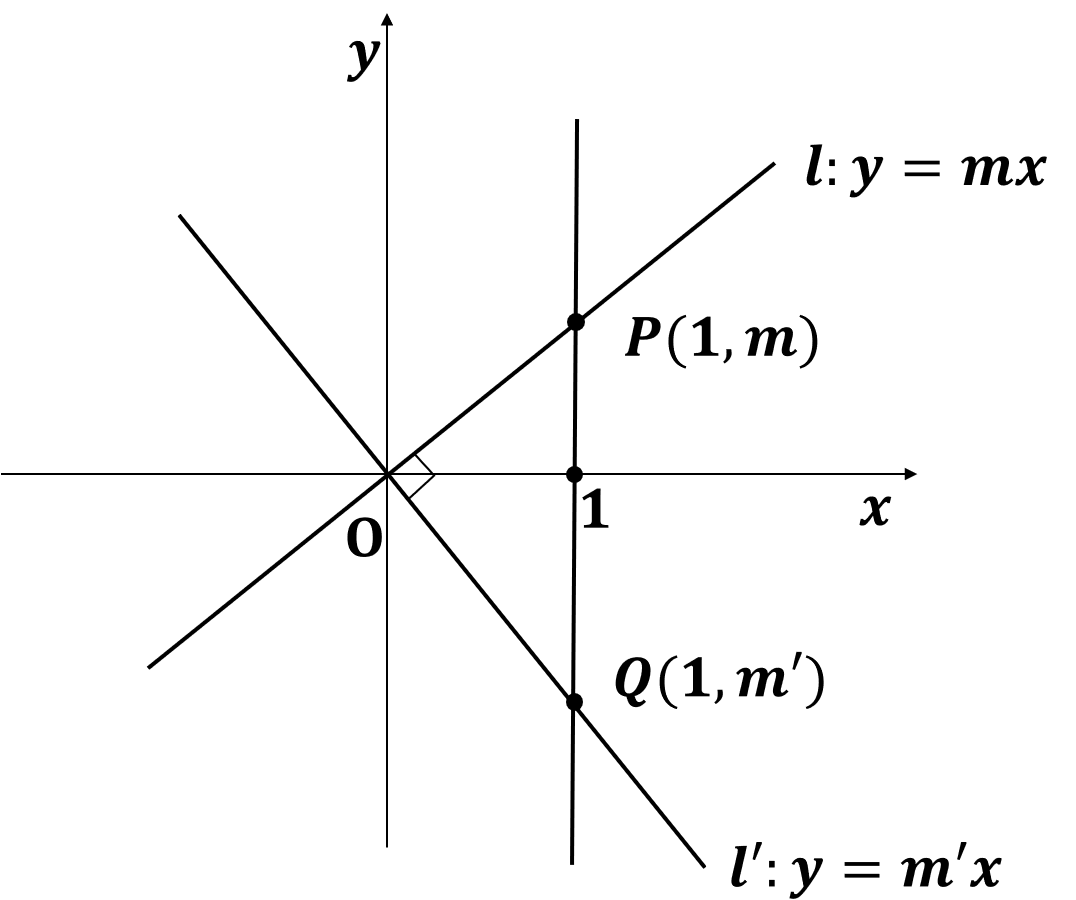
위 그림과 같이 원점을 지나고 서로 수직인 두 직선을 긋고 직선 x=1을 그으면 교점 P, Q가 만들어지고 위에 표시된 좌표를 가지게 된다. 그리고 삼각형 △POQ가 만들어지고 ∠POQ = 90° 이므로 피타고라스의 정리를 활용할 수 있다.
정리해보자.

이 내용은 증명과정 보단 결과가 이용되는 경우가 참 많으니 그냥 이렇게 증명할 수 있구나 정도로만 기억하고 넘어가자.
※같이 보기
반응형
'수학이야기 > 공식 모음' 카테고리의 다른 글
| 자취의 방정식에 대하여 알아보자. (0) | 2021.11.12 |
|---|---|
| 점과 직선사이의 거리 공식 및 증명하기 (0) | 2021.11.11 |
| 직선의 방정식 공식 및 증명하기 (0) | 2021.11.09 |
| 내접원의 반지름 길이를 알 때 삼각형의 넓이 구하기 (0) | 2021.11.08 |
| 평면 위의 두 점 사이의 거리 공식 및 증명(유도과정) (0) | 2021.11.03 |