반응형

| 내접원의 반지름의 길이를 알 때 삼각형의 넓이 |
삼각형에 내접하는 원의 반지름을 알 경우 간단한 방법으로 삼각형의 넓이를 구할 수 있다.

위와 같이 내접원의 반지름의 길이가 r이고 각 변의 길이가 a, b, c인 삼각형이 주어졌을 때 삼각형의 넓이는 아래와 같이 나타낼 수 있다.
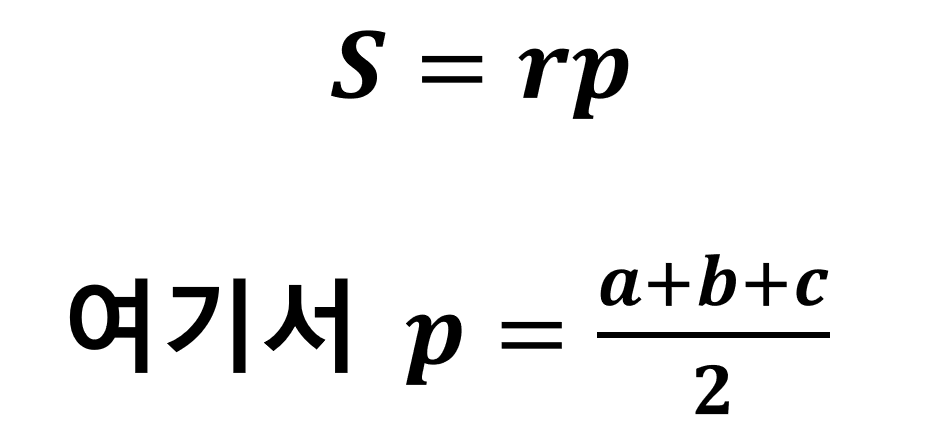
| 공식 유도하기 |
조금만 생각해보면 이 공식은 그리 어렵게 유도되는 공식이 아니라는 것을 알 수 있다.

위 그림와 같이 △ABC의 내접원의 중심을 I, 반지름의 길이를 r이라고 하면 △ABC의 넓이는 각 밑변이 a, b, c이고 높이가 r인 삼각형 3개의 넓이의 합이라고 말할 수 있다. 이것을 풀어쓰면 공식이 완성된다.

가끔 고난이도 문제에서 조커 같은 역할을 하는 공식이기도 하다. 실전에서 중요한 것을 공식 자체를 기억해내는 것보다 공식이 나온 개념과 원리를 떠올리는 것이다. 잘 숙지하도록 하자.
반응형
'수학이야기 > 공식 모음' 카테고리의 다른 글
| 두 직선이 수직일 조건과 증명하기 (0) | 2021.11.10 |
|---|---|
| 직선의 방정식 공식 및 증명하기 (0) | 2021.11.09 |
| 평면 위의 두 점 사이의 거리 공식 및 증명(유도과정) (0) | 2021.11.03 |
| 세 변의 길이를 알 때, 삼각형의 넓이 구하기[헤론의 공식] (0) | 2021.11.02 |
| 제2코사인법칙 공식 및 유도과정 (2) | 2021.11.01 |