
| 공식은 만들 수 있다. |
수학에서는 무수히 많은 공식들이 있다. 정확하게 말하면 무수히 많은 공식들을 만들 수 있다. 극단적인 예를 들면 임의의 수 a에 이와 같은 크기의 수를 더한 값(a + a)을 구하는 공식은 2a다. 이것을 보고 정말 어이가 없다 이게 무슨 공식이냐라고 말하는 사람도 있을 것이다. 하지만 이것은 공식이라고 말할 수 있다. 다만 공식화할 필요가 없을 정도로 너무나도 간단하거나 생각하기 쉬운 내용이기 때문이다. 아주 오래전부터 수많은 공식들이 만들어졌고 그중 정말 편리하고 유용하게 쓰이는 것들이 지금까지 내려와 우리의 교과과정에 실리게 되었다고 생각하면 된다.
서론이 좀 길었지만 내가 지금 이 이야기를 한 이유는 정육각형 넓이 공식은 위와 같은 논리와 다르지 않다는 것을 말하는 것이다. 공식화를 할 필요가 없을 정도로 생각하기 쉬운 것이 정육각형 넓이 공식이다. 몰라도 수학 시험을 치는데는 전혀 지장이 없다.
| 정육각형 넓이 공식 및 유도 |

몰라도 되는 공식이라 해도 알아서 나쁠건 전혀 없다. 아는 것이 힘이라는 말도 있으니 정육각형 넓이 공식에 대하여 알아보도록 하겠다. 한 변의 길이가 a인 정육각형의 넓이를 구해보자.

▲위 그림과 같이 대각선을 그으면 한 변의 길이가 a인 정삼각형 6개가 만들어진다. 즉 한 변의 길이가 a인 정삼각형 6개의 넓이를 합친 게 정육각형의 넓이라는 소리다. 정삼각형 넓이 공식에 6을 곱하면 정육각형 넓이 공식이 만들어지는 것이다.
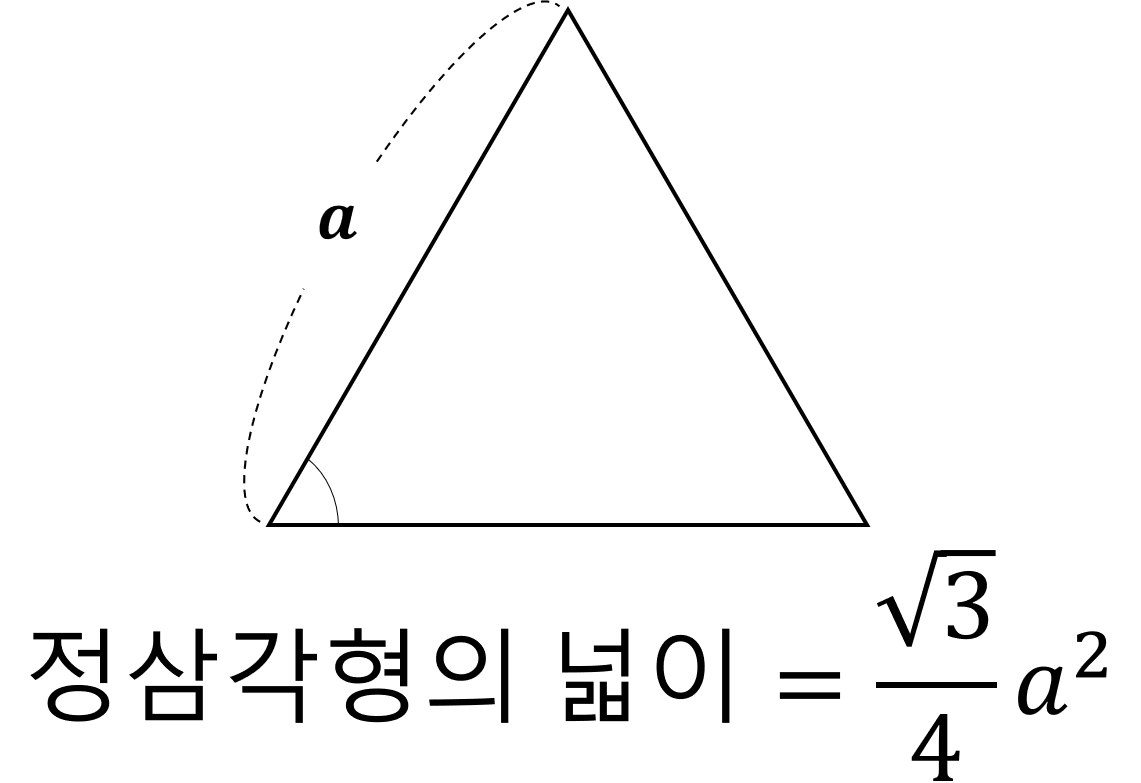
▲정삼각형의 넓이 공식은 위와 같다. 정삼각형 넓이 공식을 잘 모르겠다면 아래의 글을 참조하자.
2021.10.15 - [수학이야기/공식 모음] - 정삼각형의 넓이 공식 및 유도
정삼각형의 넓이 공식 및 유도
개요 한 변의 길이를 알고 있다면 정삼각형의 높이와 넓이를 구할 수 있으며 공식화를 할 수 있다. 어떻게 구하는지 알아보자. 공식 그림과 같이 정삼각형의 한 변의 길이가 a인 경우 높이와 넓
houseofj.tistory.com

▲정삼각형의 넓이 공식에 6를 곱하면 위와 같이 정육각형 넓이의 공식이 만들어진다. 이 글을 읽고 정육각형 넓이 공식을 외워가는 것도 좋지만, 무언가를 구하기 위해 저렇게 사고하는 습관을 가져야겠다는 생각을 가졌다면 공식보다 더 큰 수확이라고 생각된다.
'수학이야기 > 공식 모음' 카테고리의 다른 글
| 세 점이 일직선 위에 있을 조건 (0) | 2022.05.28 |
|---|---|
| 정팔각형 넓이 공식 및 유도하는 방법 (0) | 2022.04.30 |
| 삼수선의 정리와 증명하는 방법 (0) | 2022.04.01 |
| 직육면체 대각선 길이 공식 및 증명하기 (0) | 2021.12.15 |
| 정사각뿔 높이, 겉넓이, 부피 구하는 공식 및 증명 (0) | 2021.12.14 |